 por Claudin » Seg Mai 23, 2011 18:43
por Claudin » Seg Mai 23, 2011 18:43
![\lim_{x\rightarrow+\infty}\frac{\frac{1}{x^6}+(x^{-4})^2-(14x^3)^{-5}}{\frac{(x^{20})^{-1}}{(\sqrt[6]{x^{20})}^{-1}}+\sqrt[5]{4x^6}} \lim_{x\rightarrow+\infty}\frac{\frac{1}{x^6}+(x^{-4})^2-(14x^3)^{-5}}{\frac{(x^{20})^{-1}}{(\sqrt[6]{x^{20})}^{-1}}+\sqrt[5]{4x^6}}](/latexrender/pictures/7383706c8dc7363144435e556cca93ca.png)
Nao consegui concluir o exercicio
algm para ajudar?
obrigado
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Seg Mai 23, 2011 18:49
por Claudin » Seg Mai 23, 2011 18:49
viewtopic.php?f=120&t=4846viewtopic.php?f=120&t=4844esses dois topicos tbm
ainda n foram respondidos!
obrigado
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Qua Mai 25, 2011 17:49
por Claudin » Qua Mai 25, 2011 17:49
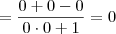
A terceira parte da resolução, exatamente no denominador não consegui compreender os cálculos Luiz!
obs:
![(\frac{x^{20}}{\sqrt[6]{x^{20}}})^{-1} (\frac{x^{20}}{\sqrt[6]{x^{20}}})^{-1}](/latexrender/pictures/f41782bdb5418f031ed4f6a0731055cd.png)
no denominador do enunciado o valor correto seria esse
mas nao causa nenhuma mudança ne?
Abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qua Mai 25, 2011 19:51
por LuizAquino » Qua Mai 25, 2011 19:51
Ao que parece você não revisou os conteúdos de potenciação e radiciação como eu recomendei. Se você não fizer essa revisão, então muito provavelmente vai continuar errando exercícios como esse.
Usando propriedades de potenciação, sendo
a e
b não nulos, sabemos que
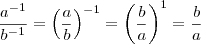
.
Além disso, usando propriedades de radiciação, sendo
a positivo e
b não nulo, sabemos que
![\frac{\sqrt[n]{a}}{b} = \sqrt[n]{\frac{a}{b^n}} \frac{\sqrt[n]{a}}{b} = \sqrt[n]{\frac{a}{b^n}}](/latexrender/pictures/008eb28d9eff1c44eb73c413942a828c.png)
,
sendo que
b deve ser positivo não nulo caso
n seja par.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qua Mai 25, 2011 19:53
por Claudin » Qua Mai 25, 2011 19:53
Só nao consegui chegar em
![\sqrt[6]{\frac{1}{x^{100}}}+1 \sqrt[6]{\frac{1}{x^{100}}}+1](/latexrender/pictures/ca82711f044690481f21c9435294b92a.png)
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qua Mai 25, 2011 20:27
por LuizAquino » Qua Mai 25, 2011 20:27
Não há mistério algum. Após utilizar as propriedades de potenciação e radiciação, basta dividir tanto o numerador quanto o denominador pela expressão
![\sqrt[5]{4x^6} \sqrt[5]{4x^6}](/latexrender/pictures/165ff28f72d8c1ec592a8810e2fc198c.png)
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qui Mai 26, 2011 11:31
por Claudin » Qui Mai 26, 2011 11:31
![\sqrt[6]{\frac{x^{20}}{(x^{20})^{6}}} . \frac{1}{\sqrt[5]{4x^6}} + 1 \sqrt[6]{\frac{x^{20}}{(x^{20})^{6}}} . \frac{1}{\sqrt[5]{4x^6}} + 1](/latexrender/pictures/9caf56e5af9bddadc0e5c22549089be5.png)
cheguei ate essa parte!
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por FilipeCaceres » Qui Mai 26, 2011 22:28
por FilipeCaceres » Qui Mai 26, 2011 22:28
Observe que,
![\sqrt[6]{\frac{x^{20}}{(x^{20})^{6}}}=\sqrt[6]{\frac{x^{20}}{x^{20.6}}}=\sqrt[6]{\frac{x^{20}}{x^{120}}}=\sqrt[6]{\frac{1}{x^{120-20}}}=\sqrt[6]{\frac{1}{x^{100}}} \sqrt[6]{\frac{x^{20}}{(x^{20})^{6}}}=\sqrt[6]{\frac{x^{20}}{x^{20.6}}}=\sqrt[6]{\frac{x^{20}}{x^{120}}}=\sqrt[6]{\frac{1}{x^{120-20}}}=\sqrt[6]{\frac{1}{x^{100}}}](/latexrender/pictures/9019b2dae85bad74dc0f03dbd68a3d7d.png)
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Claudin » Qui Mai 26, 2011 22:33
por Claudin » Qui Mai 26, 2011 22:33
Nossa, claro! Tava na cara e não percebi.
eu tava deixando
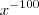
e não retirei a potência por isso nao estava encontrando o resultado!
Valeu pela explicaçao Filipe
Abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6484 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4568 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 4863 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7044 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4277 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow+\infty}\frac{\frac{1}{x^6}+(x^{-4})^2-(14x^3)^{-5}}{\frac{(x^{20})^{-1}}{(\sqrt[6]{x^{20})}^{-1}}+\sqrt[5]{4x^6}} \lim_{x\rightarrow+\infty}\frac{\frac{1}{x^6}+(x^{-4})^2-(14x^3)^{-5}}{\frac{(x^{20})^{-1}}{(\sqrt[6]{x^{20})}^{-1}}+\sqrt[5]{4x^6}}](/latexrender/pictures/7383706c8dc7363144435e556cca93ca.png)

![\lim_{x\rightarrow+\infty}\frac{\frac{1}{x^6}+(x^{-4})^2-(14x^3)^{-5}}{\frac{(x^{20})^{-1}}{(\sqrt[6]{x^{20})}^{-1}}+\sqrt[5]{4x^6}} \lim_{x\rightarrow+\infty}\frac{\frac{1}{x^6}+(x^{-4})^2-(14x^3)^{-5}}{\frac{(x^{20})^{-1}}{(\sqrt[6]{x^{20})}^{-1}}+\sqrt[5]{4x^6}}](/latexrender/pictures/7383706c8dc7363144435e556cca93ca.png)


![\lim_{x\to +\infty}\frac{\frac{1}{x^6}+(x^{-4})^2-(14x^3)^{-5}}{\frac{(x^{20})^{-1}}{(\sqrt[6]{x^{20}})^{-1}}+\sqrt[5]{4x^6}} \lim_{x\to +\infty}\frac{\frac{1}{x^6}+(x^{-4})^2-(14x^3)^{-5}}{\frac{(x^{20})^{-1}}{(\sqrt[6]{x^{20}})^{-1}}+\sqrt[5]{4x^6}}](/latexrender/pictures/cfeb68536e8b581f9e864d80553d9064.png)
![\,= \lim_{x\to +\infty}\frac{\frac{1}{x^6}+\frac{1}{x^8}-\frac{1}{14^5x^{15}}}{\frac{\sqrt[6]{x^{20}}}{x^{20}}+\sqrt[5]{4x^6}} \,= \lim_{x\to +\infty}\frac{\frac{1}{x^6}+\frac{1}{x^8}-\frac{1}{14^5x^{15}}}{\frac{\sqrt[6]{x^{20}}}{x^{20}}+\sqrt[5]{4x^6}}](/latexrender/pictures/9de2bfefc652dca3ed98d6bb1123b2f9.png)
![= \lim_{x\to +\infty}\frac{\frac{1}{x^6\sqrt[5]{4x^6}}+\frac{1}{x^8\sqrt[5]{4x^6}}-\frac{1}{14^5x^{15}\sqrt[5]{4x^6}}}{\frac{1}{\sqrt[5]{4x^6}}\sqrt[6]{\frac{1}{x^{100}}}+1} = \lim_{x\to +\infty}\frac{\frac{1}{x^6\sqrt[5]{4x^6}}+\frac{1}{x^8\sqrt[5]{4x^6}}-\frac{1}{14^5x^{15}\sqrt[5]{4x^6}}}{\frac{1}{\sqrt[5]{4x^6}}\sqrt[6]{\frac{1}{x^{100}}}+1}](/latexrender/pictures/e3f266ebc49a220bcf63c4c5dd23ca0c.png)

![(\frac{x^{20}}{\sqrt[6]{x^{20}}})^{-1} (\frac{x^{20}}{\sqrt[6]{x^{20}}})^{-1}](/latexrender/pictures/f41782bdb5418f031ed4f6a0731055cd.png)

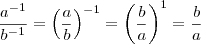 .
.![\frac{\sqrt[n]{a}}{b} = \sqrt[n]{\frac{a}{b^n}} \frac{\sqrt[n]{a}}{b} = \sqrt[n]{\frac{a}{b^n}}](/latexrender/pictures/008eb28d9eff1c44eb73c413942a828c.png) ,
,
![\sqrt[6]{\frac{1}{x^{100}}}+1 \sqrt[6]{\frac{1}{x^{100}}}+1](/latexrender/pictures/ca82711f044690481f21c9435294b92a.png)

![\sqrt[5]{4x^6} \sqrt[5]{4x^6}](/latexrender/pictures/165ff28f72d8c1ec592a8810e2fc198c.png) .
.
![\sqrt[6]{\frac{x^{20}}{(x^{20})^{6}}} . \frac{1}{\sqrt[5]{4x^6}} + 1 \sqrt[6]{\frac{x^{20}}{(x^{20})^{6}}} . \frac{1}{\sqrt[5]{4x^6}} + 1](/latexrender/pictures/9caf56e5af9bddadc0e5c22549089be5.png)

![\sqrt[6]{\frac{x^{20}}{(x^{20})^{6}}}=\sqrt[6]{\frac{x^{20}}{x^{20.6}}}=\sqrt[6]{\frac{x^{20}}{x^{120}}}=\sqrt[6]{\frac{1}{x^{120-20}}}=\sqrt[6]{\frac{1}{x^{100}}} \sqrt[6]{\frac{x^{20}}{(x^{20})^{6}}}=\sqrt[6]{\frac{x^{20}}{x^{20.6}}}=\sqrt[6]{\frac{x^{20}}{x^{120}}}=\sqrt[6]{\frac{1}{x^{120-20}}}=\sqrt[6]{\frac{1}{x^{100}}}](/latexrender/pictures/9019b2dae85bad74dc0f03dbd68a3d7d.png)

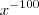 e não retirei a potência por isso nao estava encontrando o resultado!
e não retirei a potência por isso nao estava encontrando o resultado!