Relações entre 2 números

[leocadio]

Tenho 2 números, o primeiro é 555.657.585.960, e o segundo é 10.203.040.506.
O primeiro, dividido por 545.454.545.454 dá o resultado de 1,01870557426
O segundo, dividido por 545.454.545.454 dá o resultado de 0,01870557426

Sou leigo em matemática (sou médico) e gostaria de saber o significado, se é que há significado, de dois números tão diferentes terem como resultado, com o mesmo divisor, números idênticos nas decimais, diferindo apenas pelo 1 inteiro.

Agradeço pela atenção
Leocádio

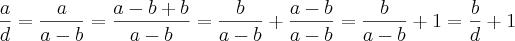
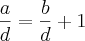[Neperiano]

Ola

Sou aluno de ensino médio.

Mas acredito que de o mesmo resultado nos decimais por ter dividido pelo mesmo numero

Abraços

[leocadio]

Você pode pegar outros números, quantos quiser, e dividi-los pelo número 545.454.545.454, jamais encontrará um resultado com as mesmas decimais!

[Sandra Piedade]

Olá

Fiz umas contas rápidas e concluí que por exemplo, dados 3 e 33, 3:30=0.1 e 33:30=1.1, as partes decimais também são iguais, mas finitas. Depois experimentei com valores que davam dízimas infinitas periódicas e reparei que isto se devia a que o terceiro número (545.454.545.454) é igual à diferença entre os outros dois, isto é: 545.454.545.454=555.657.585.960-10.203.040.506. De uma forma geral, quando temos dois números "a" e "b", e se a-b=d, então



concluímos assim que

,

porque d (o divisor) é igual à diferença entre os números de partida.

Se experimentar escolher dois números inteiros quaisquer a e b, calcular a sua diferença e depois dividir ambos por esse valor, concluirá que os dois quocientes têm iguais partes decimais.

Espero ter conseguido esclarecer!