 por abel » Sáb Nov 01, 2008 23:24
por abel » Sáb Nov 01, 2008 23:24
Oi pessoal,
eu meio que tô perturbardo com uma questão aqui...
é uma função do segundo grau f(x) = -x² + 62x - 600
só q eles pedem pra eu achar as raízes dessa função... o problema é que seu eu for perder tempo fazendo baskara com esses números enormes num vestibular por exemplo, eu tô ferrado O.o
tem um jeito de saber as raízes de uma maneira mais fácil?
-
abel
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Out 26, 2008 19:15
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Farmácia
- Andamento: cursando
 por admin » Dom Nov 02, 2008 00:05
por admin » Dom Nov 02, 2008 00:05
Olá
abel, boas-vindas!
Normalmente em questões de vestibulares, mesmo com números "grandes", as contas não são tão complicadas.
Mas neste caso sim, há uma maneira mais fácil, considerando a
soma e o produto das raízes.
Se a função é
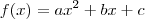
E

e
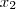
são as raízes, temos que a soma é:
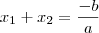
Produto:
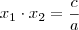
Aqui há um tópico onde comentei sobre como obter estas "fórmulas":
http://www.ajudamatematica.com/viewtopic.php?f=105&t=127&p=216#p216Ou seja, você precisa tentar descobrir as raízes sabendo a soma e o produto:
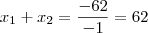
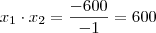
Em palavras, você deve se perguntar assim: quais os dois números que somados resultam em
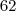
e multiplicados resultam em
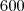
?
Nem sempre é imediato inferir sobre eles, mas neste caso é simples.
Espero ter ajudado.
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Molina » Seg Nov 03, 2008 15:29
por Molina » Seg Nov 03, 2008 15:29
Neste caso soma e produto (forma repassada pelo fábio) não nos ajuda muito, já que os dois valores são alto (62 e 600). Para números menores é sempre bem eficiente este método.
Sugiro tentar resolver por Báskara mas antes multiplique toda a equação por -1 para ficar com o primeiro termo positivo.
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por admin » Seg Nov 03, 2008 16:04
por admin » Seg Nov 03, 2008 16:04
Olá.
Ainda acho que ajuda, vou tentar argumentar...

Começando o teste com

e
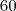
logo se chega às raízes, considerando que a soma atual é
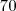
e precisamos diminuí-la.
Mas, outra dica para facilitar ainda mais caso não descubra é fatorar
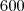
:

Como o produto é

, basta combinarmos estes fatores buscando a soma
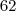
, assim limitamos bem os números candidatos.
Até mais!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por abel » Seg Nov 03, 2008 19:06
por abel » Seg Nov 03, 2008 19:06
Por báskara eu achei muito cansativo e que consome muito tempo.
tentei fazer pelo método do fábio... mas não tinah idéia de como achar dois números q multiplicassem e somassem valores altos desse jeito...
o fábio disse em fatorar e combinar os fatores... mas eu não entendi direito como isso funciona. =/
-
abel
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Out 26, 2008 19:15
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Farmácia
- Andamento: cursando
 por admin » Ter Nov 04, 2008 04:31
por admin » Ter Nov 04, 2008 04:31
Olá
abel!
Temos que primeiro considerar o produto, com os números permitidos provenientes da fatoração.
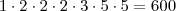
Exemplos de combinações com os fatores:
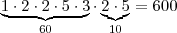
Soma:
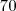
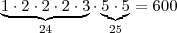
Soma:
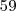
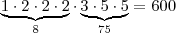
Soma:


Podemos desconsiderar aquelas combinações de fatores cuja soma evidentemente já excede
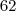
.
Assim não demora muito para encontrarmos as raízes.
abel, comente se ficou claro...
Se não preferir assim, a opção será "Bhaskara".
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por admin » Ter Nov 04, 2008 04:31
por admin » Ter Nov 04, 2008 04:31
Olá
abel!
Temos que primeiro considerar o produto, com os números permitidos provenientes da fatoração.
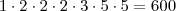
Exemplos de combinações com os fatores:
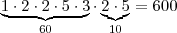
Soma:
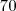
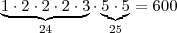
Soma:
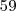
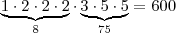
Soma:


Podemos desconsiderar aquelas combinações de fatores cuja soma evidentemente já excede
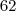
.
Assim não demora muito para encontrarmos as raízes.
abel, comente se ficou claro...
Se não preferir assim, a opção será "Bhaskara".
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo de raizes de uma função
 por EREGON » Sex Nov 14, 2014 14:22
por EREGON » Sex Nov 14, 2014 14:22
- 2 Respostas
- 2282 Exibições
- Última mensagem por adauto martins

Seg Jan 19, 2015 09:56
Funções
-
- [FUNÇÃO QUADRÁTICA] Comparação de raízes
por STARK » Sex Dez 18, 2015 20:39
- 1 Respostas
- 2452 Exibições
- Última mensagem por Russman

Qua Dez 23, 2015 22:29
Funções
-
- FUNÇAO DE SEGUNDO GRAU A PARTIR DE RAIZES, ETC.
por aspirantestudante » Ter Set 14, 2010 15:58
- 11 Respostas
- 8377 Exibições
- Última mensagem por MarceloFantini

Seg Out 11, 2010 14:19
Funções
-
- [Função modular] Dúvida com relação a raízes
por exburro » Sáb Mar 31, 2012 01:23
- 1 Respostas
- 2600 Exibições
- Última mensagem por LuizAquino

Sex Abr 06, 2012 12:40
Funções
-
- Dúvida em exercício - raízes de função quadrática
por Danilo » Qui Jun 07, 2012 01:50
- 1 Respostas
- 3190 Exibições
- Última mensagem por Russman

Qui Jun 07, 2012 03:32
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


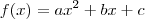
 e
e 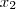 são as raízes, temos que a soma é:
são as raízes, temos que a soma é: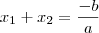
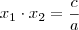
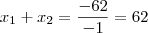
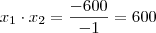
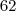 e multiplicados resultam em
e multiplicados resultam em 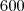 ?
?



 e
e 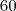 logo se chega às raízes, considerando que a soma atual é
logo se chega às raízes, considerando que a soma atual é 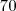 e precisamos diminuí-la.
e precisamos diminuí-la.
 , basta combinarmos estes fatores buscando a soma
, basta combinarmos estes fatores buscando a soma 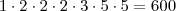
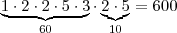
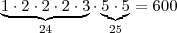
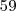
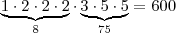




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.