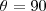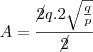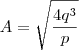por maria cleide » Qui Mai 19, 2011 12:35
por maria cleide » Qui Mai 19, 2011 12:35
Considere a função quadrática
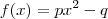
e
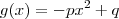
, onde p e q são números reais não nulos. A área do quadrilátero que tem como vértices os pontos de intersecção dos gráficos com os eixos coordenados vale:
A-( )
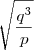
B-( )
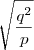
C-( )
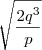
D-( )
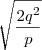
E-( )
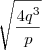
Como fiz: Apliquei a fórmula de bhaskara e encontrei as raizes:
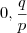
. Mas agora não sei continuar
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por FilipeCaceres » Qui Mai 19, 2011 14:26
por FilipeCaceres » Qui Mai 19, 2011 14:26
Temos
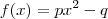
e
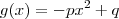
Para encontrar o ponto de intersecção do gráfico com as coordenadas, basta calcular
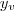
Para f(x) temos:

Para g(x) temos:

A distância de
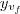
até
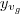
corresponde a uma das diagonais, para encontrar a outra diagonal devemos encontrar a intersecção entre os gráficos,para isso façamos f(x)=g(x),então temos,

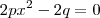
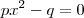
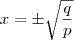
Sabendo as diagonais é fácil calcular a área de um quadrilátero, supondo que "a" e "b" são nossas diagonais e que

seja o angulo entre elas temos que a área do nosso quadrilátero é calculo por:
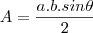
Agora observe que tanto os valores de
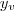
quanto os valores

estão sobre os eixo das coordenadas e abscissas respectivamente, e desta forma o nosso valor de
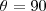
Assim temos,
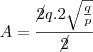
Portanto,
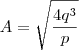
Espero que seja isso.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função quadrática
por Ananda » Sex Mar 28, 2008 16:00
- 6 Respostas
- 9024 Exibições
- Última mensagem por admin

Sex Mar 28, 2008 21:25
Funções
-
- Função quadratica
por Aline » Qui Jun 18, 2009 14:22
- 2 Respostas
- 2531 Exibições
- Última mensagem por Cleyson007

Sex Jun 19, 2009 10:00
Funções
-
- Função Quadratica
por Aline » Qui Jun 18, 2009 14:37
- 1 Respostas
- 1936 Exibições
- Última mensagem por Marcampucio

Qui Jun 18, 2009 16:45
Funções
-
- Função Quadratica
por Aline » Sáb Jun 20, 2009 18:23
- 1 Respostas
- 2016 Exibições
- Última mensagem por Molina

Dom Jun 21, 2009 20:28
Funções
-
- Função Quadratica
 por guijermous » Sáb Abr 10, 2010 10:02
por guijermous » Sáb Abr 10, 2010 10:02
- 4 Respostas
- 7897 Exibições
- Última mensagem por Molina

Sáb Abr 10, 2010 16:27
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
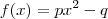 e
e 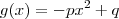 , onde p e q são números reais não nulos. A área do quadrilátero que tem como vértices os pontos de intersecção dos gráficos com os eixos coordenados vale:
, onde p e q são números reais não nulos. A área do quadrilátero que tem como vértices os pontos de intersecção dos gráficos com os eixos coordenados vale: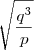
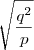
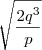
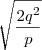
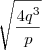
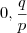 . Mas agora não sei continuar
. Mas agora não sei continuar

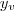


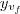 até
até 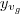 corresponde a uma das diagonais, para encontrar a outra diagonal devemos encontrar a intersecção entre os gráficos,para isso façamos f(x)=g(x),então temos,
corresponde a uma das diagonais, para encontrar a outra diagonal devemos encontrar a intersecção entre os gráficos,para isso façamos f(x)=g(x),então temos,
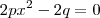
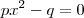
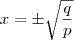
 seja o angulo entre elas temos que a área do nosso quadrilátero é calculo por:
seja o angulo entre elas temos que a área do nosso quadrilátero é calculo por: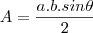
 estão sobre os eixo das coordenadas e abscissas respectivamente, e desta forma o nosso valor de
estão sobre os eixo das coordenadas e abscissas respectivamente, e desta forma o nosso valor de