 por TheoFerraz » Seg Mai 16, 2011 20:39
por TheoFerraz » Seg Mai 16, 2011 20:39
Na lista de exercicios o professor pegou esse exercicio de um livro ai:
Seja
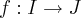
uma função bijetora. prove que ela é ou crescente, ou decrescente (monótona)
a) pelo método da análise real.
b) pelo método das derivadas.
Olha, talvez eu até consiga por derivadas, mas eu mal sei o que é bijetora! se alguém puder me ajudar seria ótimo!
Ah, e sobre essas demonstrações ai, principalmente as analíticas, existe algum livro, algum lugar que eu possa aprender essas coisas? como provar por absurdo, indução finita, essas coisas? Eu faço física mas o meu professor da a aula como se nós fizéssemos matemática pedindo para provarmos teoremas e etc, mas eu preciso saber essas coisas...
Agradeço já à qualquer ajuda! Obrigado!
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por LuizAquino » Qua Mai 18, 2011 12:34
por LuizAquino » Qua Mai 18, 2011 12:34
Dizemos que a função
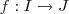
é bijetora se
as duas propriedades abaixo são válidas:
(i) Para quaisquer

e
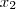
pertencentes a
I, se
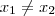
, então temos que
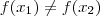
;
(ii) Para qualquer y pertencente a
J, temos que existe algum x pertencente a
I tal que y = f(x).
Se uma função tem
apenas a propriedade (i), então ela é chamada de injetora.
Por outro lado, se uma função tem
apenas a propriedade (ii), então ela é chamada de sobrejetora.
Para resolver o quesito (a) do exercício uma boa alternativa é usar o Axioma da Tricotomia (juntamente com o fato da função ser injetora): dados dois números reais
a e
b apenas uma das afirmações será verdadeira:
(i)
a =
b(ii)
a >
b(iii)
a <
bQuanto a livros com técnicas de demonstração há vários. Um deles é:
Fossa, John. Introdução às Técnicas de Demonstração na Matemática. 2ª Edição. São Paulo: Editora Livraria da Física, 2009.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Funcao] Decrescente ou crescente
 por Apprentice » Dom Set 30, 2012 22:34
por Apprentice » Dom Set 30, 2012 22:34
- 3 Respostas
- 2322 Exibições
- Última mensagem por vitor_jo

Qua Jan 21, 2015 06:01
Funções
-
- [Função Crescente e Decrescente Gráfico ]
 por soccol » Seg Out 06, 2014 23:27
por soccol » Seg Out 06, 2014 23:27
- 0 Respostas
- 1051 Exibições
- Última mensagem por soccol

Seg Out 06, 2014 23:27
Funções
-
- PA crescente
por jose henrique » Dom Set 19, 2010 12:23
- 2 Respostas
- 3570 Exibições
- Última mensagem por MarceloFantini

Seg Set 20, 2010 03:14
Sequências
-
- PG Crescente
por Lana Brasil » Seg Mai 27, 2019 21:21
- 2 Respostas
- 5513 Exibições
- Última mensagem por Lana Brasil

Qua Mai 29, 2019 09:45
Progressões
-
- [PG infinita e crescente]
por JKS » Qui Abr 11, 2013 01:38
- 1 Respostas
- 2101 Exibições
- Última mensagem por DanielFerreira

Ter Abr 16, 2013 12:52
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
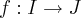 uma função bijetora. prove que ela é ou crescente, ou decrescente (monótona)
uma função bijetora. prove que ela é ou crescente, ou decrescente (monótona)

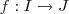 é bijetora se
é bijetora se  e
e 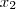 pertencentes a
pertencentes a 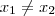 , então temos que
, então temos que 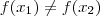 ;
;
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.