Problema de área cirular (URGENTE)

[antoniapires]

Alguém pode me ajudar neste exercício?

não consigo resolver, é URGENTE!

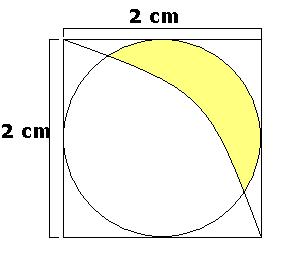
problema de geometria.JPG (9.65 KiB) Exibido 5009 vezes

[Neperiano]

Ola

Eu naum sei qual a sua duvida, mas se é o raio é simples, se você analisar que de um lado ao outro do circulo é 2 cm então a metade é o raio.

Caso sua duvida seja outra poste aqui perguntando.

Abraços

[antoniapires]

Eu preciso calcular a aréa amarela, mas nao sei como faço isso! já que depois eu tenho que tirar a area dos espacinhos em branco :S

[admin]

Olá antoniapires, boas-vindas!

É necessário que você envie também o enunciado deste problema para definir adequadamente a figura.

Repare que com rigorosidade, apenas com esta figura, ficam as dúvidas:
-como não há ângulos informados no quadrilátero, não sabemos se é de fato quadrado;
-conseqüentemente, não sabemos se a curva inscrita neste quadrilátero é de fato uma circunferência;
-e ainda, não sabemos sobre a curva secante à "aparente circunferência".