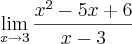
resolvendo normalmente
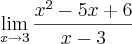 ---->
----> 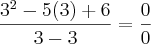
ou seja, caindo em uma indeterminaçao, minha dúvida é a seguinte
sempre quando eu pegar um limite pra resolver eu tento resolver normalmente como tentei acima
ai resultando em uma indeterminação, q eu devo procurar outros meios?
Por exemplo eu poderia resolver por produto notavel
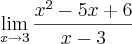 --->
---> 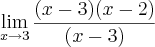 -->
--> 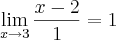
Porém tentei resolver tambem, dividindo tanto o numerador como o denominador por x
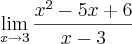 --->
---> 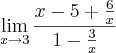 ---->
----> 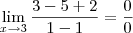
No meu modo de ver, o resultado do limite teria de ser o mesmo, porém nao foi!
Entao gostaria de saber qual forma devo procurar resolver limite , sempre, e qual nao devo usar.
obrigado


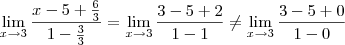
 novamente, desta forma dividir por x não foi a melhor coisa a se fazer, o mais simples seria fatorar ou então utilizar L'Hôpital.
novamente, desta forma dividir por x não foi a melhor coisa a se fazer, o mais simples seria fatorar ou então utilizar L'Hôpital.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)