Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por Neperiano » Qua Fev 11, 2009 18:32
por Neperiano » Qua Fev 11, 2009 18:32
Ola
Como prometi vou postar aqui algumas questões do Vestibular 2008 da UFRGS, terceiro melhor do Brasil, cuja prova de Matemática é considerada a mais Dificel.
Ai vai:
1 - O custo de uma embalagem é diretamente proporcional à superfície do sólido que se deseja embalar. Se o custo para embalar um cubo de 40 cm de aresta é R$10,00, a embalagem de um cubo de 80 cm de aresta custa, em reais,
(A) 15.
(B) 20.
(C) 25.
(D) 40.
(E) 80.
2 - Em março de 2007, o menor preço oferecido por uma companhia telefônica para uma ligação do Brasil para os Estados Unidos era de R$0,95 o minuto. O mesmo serviço pela internet custava R$0,05 o minuto e mais R$0,10 da taxa de conexão da chamada. Em ambas as situações, o preço por segundo correspondia a do preço por minuto.
Nessas condições, para que uma ligação telefônica, do Brasil para os Estados Unidos, tivesse um custo menor via companhia telefônica do que via internet, a duração dessa ligação deveria ser, em número inteiro de segundos, no máximo, de
(A) 6.
(B) 7.
(C) 8.
(D) 9.
(E) 10.
3 - Um hexágono regular tem lado de comprimento 1. A soma dos quadrados de todas as suas diagonais é
(A) 6.
(B) 12.
(C) 18.
(D) 24.
(E) 30.
4 - Numa seqüência de quadrados, o primeiro tem lado igual a 1, e o lado de cada um dos seguintes é igual à diagonal do quadrado anterior.
A soma das áreas dos dez primeiros quadrados dessa seqüência é
(A) 1023.
(B) 1024.
(C) 2047.
(D) 2048.
(E) 4096.
5 - O polinômio p(x)=

tem
(A) apenas duas raízes reais distintas.
(B) apenas duas raízes positivas.
(C) todas as raízes positivas.
(D) quatro raízes iguais.
(E) quatro raízes distintas.
6 - Traçando-se os gráficos das funções definidas por f(x) = 2 sen x e g(x) = 16 -

e num mesmo sistema de coordenadas cartesianas ortogonais, pode-se verificar que o número de soluções da equação f(x) = g(x)é
(A) 0.
(B) 1.
(C) 2.
(D) 3.
(E) 4.
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Sáb Fev 14, 2009 05:11
por Molina » Sáb Fev 14, 2009 05:11
Boa noite, Maligno.
Como o pessoal aqui não anda com muito tempo para resolver essas questões, vou postar a solução (de todas que eu conseguir resolver):
1) Essa questão te induz a pensar que duplicando a aresta do cubo a área da superfície duplicará também. Isto não é verdade. Neste caso um cubo de 40cm de aresta tem superfície de 9600cm² (custando R$ 10,00) e um cubo de 80cm de aresta tem superfície de 38400cm², que é o quádruplo de 9600cm², ou seja, o valor deve ser multiplicado por 4 também. Com isso concluimos que custará
R$ 40,00.
2) Verificar quanto é o gasto por segundo dos dois modos de comunicação:
Telefone = 1,58333 centavos por minuto
Internet = 0,08333 centavos por minuto (porém pága-se 10 centavos da taxa)
Ou seja, utilizando 1 segundo o telefone eu gastaria apenas 1,58333 centavos e utilizando 1 segundo a internet eu gastaria 10,08333. O maior número que posso multiplicar 1,58333 para ser menor que 10,08333 é
6:
1,58333 *
6 = 9,49998 < 10,08333
1,58333 * 7 = 11,08331 > 10,08333
3) Um hexágono regular possui 3 diagonais. A diagonal de um hexágono regular é 2 vezes o tamanho do raio de um circulo circunscrito nesse polígono. O lado de um hexágono regular é igual ao raio de um circulo circunscrito nesse hexágono: LADO = RAIO (formando 6 triângulos equiláteros dentro do hexágono).
Lado = 1

Raio = 1

Diagonal = 2

2² + 2² + 2² =
124) Primeiramente quando li achei que seria o problema mais difícil dessa lista. Mas não, é bem simples: Começando pelo primeiro quadrado de lado 1, tem-se área igual a 1 também. Lembre-se da fórmula da diagonal do quadrado, dada por
![D = \ell\:\sqrt[]{2} D = \ell\:\sqrt[]{2}](/latexrender/pictures/777e9f39975a29b503809d772846b527.png)
. Logo você percebe que a área do segundo quadrado é 2, do terceiro é 4, do quarto é 8, ... , caindo numa PG de razão 2. Usando a fórmula da soma de uma PG finita chega-se ao resultado de
1023.
5)



6) Construi o gráfico das duas, e se não errei na contrução deles eles terão apenas
2 pontos onde f(x) = g(x).
Abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por FilipeCaceres » Sex Mai 13, 2011 01:24
por FilipeCaceres » Sex Mai 13, 2011 01:24
Considerando que

seja
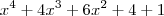
então é fácil perceber que:
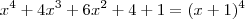
Portanto,as quatro raízes iguais.
Resposta:
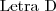
.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por rcompany » Qui Fev 21, 2019 23:21
por rcompany » Qui Fev 21, 2019 23:21
1 - O custo de uma embalagem é diretamente proporcional à superfície do sólido que se deseja embalar. Se o custo para embalar um cubo de 40 cm de aresta é R$10,00, a embalagem de um cubo de 80 cm de aresta custa, em reais,
(A) 15.
(B) 20.
(C) 25.
(D) 40.
(E) 80.
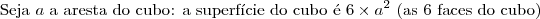
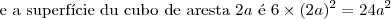

2 - Em março de 2007, o menor preço oferecido por uma companhia telefônica para uma ligação do Brasil para os Estados Unidos era de R$0,95 o minuto. O mesmo serviço pela internet custava R$0,05 o minuto e mais R$0,10 da taxa de conexão da chamada. Em ambas as situações, o preço por segundo correspondia a do preço por minuto.
Nessas condições, para que uma ligação telefônica, do Brasil para os Estados Unidos, tivesse um custo menor via companhia telefônica do que via internet, a duração dessa ligação deveria ser, em número inteiro de segundos, no máximo, de
(A) 6.
(B) 7.
(C) 8.
(D) 9.
(E) 10.

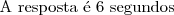
3 - Um hexágono regular tem lado de comprimento 1. A soma dos quadrados de todas as suas diagonais é
(A) 6.
(B) 12.
(C) 18.
(D) 24.
(E) 30.

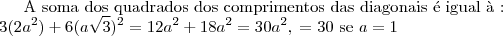
4 - Numa seqüência de quadrados, o primeiro tem lado igual a 1, e o lado de cada um dos seguintes é igual à diagonal do quadrado anterior.
A soma das áreas dos dez primeiros quadrados dessa seqüência é
(A) 1023.
(B) 1024.
(C) 2047.
(D) 2048.
(E) 4096.


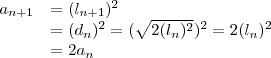

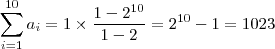
5 - O polinômio p(x)=

tem
(A) apenas duas raízes reais distintas.
(B) apenas duas raízes positivas.
(C) todas as raízes positivas.
(D) quatro raízes iguais.
(E) quatro raízes distintas.
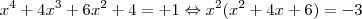
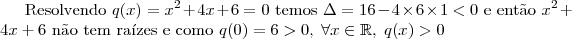
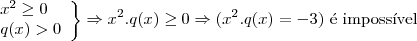
Mas achei o texto original e aí fica mais fácil ainda:

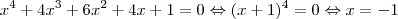
6 - Traçando-se os gráficos das funções definidas por
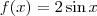
e
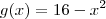
e num mesmo sistema de coordenadas cartesianas ortogonais, pode-se verificar que o número de soluções da equação f(x) = g(x)é
(A) 0.
(B) 1.
(C) 2.
(D) 3.
(E) 4.
![\phi(x)=x^2+2\sin{x}-16\\
\phi'(x)=2x+2\cos{x}\\
\phi''(x)=2-2\sin{x} \Rightarrow \forall x \in \mathbb{R},\;\phi''(x)\geq 0 \; \Rightarrow \phi' \text{ \'e crescente}\\
\left\!\!\!\!\begin{array}{r}\phi'\text{estr.crescente, continua sobre }[-\frac{\pi}{2};0]\\ \phi'(-\frac{\pi}{2})=-\pi\\ \phi'(0)=2 \end{array}\!\!\!\right\}\!\!\!\Rightarrow \!\!\exists\alpha\!\!\in ]\frac{-\pi}{2};0[\text{\'unico tal que }\phi'(\alpha)=0 \\
\phi \text{ decrescente em }]-\infty;\alpha]\text{ e crescente em }[\alpha;+\infty[\\
\phi'(\alpha)=0\Rightarrow \alpha=-\cos{\alpha}\Rightarrow \phi(\alpha)=\cos^2{\alpha}+2\sin{\alpha}-16=-\sin^2{\alpha}+2\sin{\alpha}-15\\
\text{Seja }t=\sin{\alpha}\text{ vemos que }-t^2+2t-15=0 \text{ n\~ao tem ra\'izes e } -t^2+2t-15<0\\
\text{ou seja }\phi(\alpha)<0 \phi(x)=x^2+2\sin{x}-16\\
\phi'(x)=2x+2\cos{x}\\
\phi''(x)=2-2\sin{x} \Rightarrow \forall x \in \mathbb{R},\;\phi''(x)\geq 0 \; \Rightarrow \phi' \text{ \'e crescente}\\
\left\!\!\!\!\begin{array}{r}\phi'\text{estr.crescente, continua sobre }[-\frac{\pi}{2};0]\\ \phi'(-\frac{\pi}{2})=-\pi\\ \phi'(0)=2 \end{array}\!\!\!\right\}\!\!\!\Rightarrow \!\!\exists\alpha\!\!\in ]\frac{-\pi}{2};0[\text{\'unico tal que }\phi'(\alpha)=0 \\
\phi \text{ decrescente em }]-\infty;\alpha]\text{ e crescente em }[\alpha;+\infty[\\
\phi'(\alpha)=0\Rightarrow \alpha=-\cos{\alpha}\Rightarrow \phi(\alpha)=\cos^2{\alpha}+2\sin{\alpha}-16=-\sin^2{\alpha}+2\sin{\alpha}-15\\
\text{Seja }t=\sin{\alpha}\text{ vemos que }-t^2+2t-15=0 \text{ n\~ao tem ra\'izes e } -t^2+2t-15<0\\
\text{ou seja }\phi(\alpha)<0](/latexrender/pictures/56cd4f5842222ffa3cf56bea01e2a9e4.png)
![\left \begin{array}{r}\phi\text{ continua sobre }\mathbb{R}\\
\phi\text{ estritamente decrescente sobre }]-\infty;\alpha[\\
\phi\text{ estritamente crescente sobre }]\alpha;+\infty[\\
\phi(-2\pi)>0 ,\phi(\alpha)<0,\phi(2\pi)>0 \end{array}\right \} \Rightarrow\left \{ \begin{array}{l}\exists x_1 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_1)=0\\
\exists x_2 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_2)=0\\
\forall x < -2\pi \text{ ou }x>2\pi,\;\phi(x)>0 \end{array}\right \left \begin{array}{r}\phi\text{ continua sobre }\mathbb{R}\\
\phi\text{ estritamente decrescente sobre }]-\infty;\alpha[\\
\phi\text{ estritamente crescente sobre }]\alpha;+\infty[\\
\phi(-2\pi)>0 ,\phi(\alpha)<0,\phi(2\pi)>0 \end{array}\right \} \Rightarrow\left \{ \begin{array}{l}\exists x_1 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_1)=0\\
\exists x_2 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_2)=0\\
\forall x < -2\pi \text{ ou }x>2\pi,\;\phi(x)>0 \end{array}\right](/latexrender/pictures/e541cc339277324141018ac2a21491d7.png)
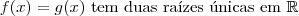
-
rcompany
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Seg Fev 18, 2019 00:57
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: administração
- Andamento: formado
Voltar para Desafios Enviados
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ufrgs
por Maria Livia » Seg Mar 18, 2013 19:18
- 3 Respostas
- 4808 Exibições
- Última mensagem por timoteo

Qua Mar 20, 2013 11:36
Geometria Plana
-
- ufrgs
por Maria Livia » Ter Set 03, 2013 12:41
- 1 Respostas
- 5561 Exibições
- Última mensagem por MateusL

Qua Set 04, 2013 11:20
Trigonometria
-
- (UFRGS)Quadrilátero
por flavio2010 » Sex Jul 16, 2010 06:36
- 1 Respostas
- 2033 Exibições
- Última mensagem por Douglasm

Sex Jul 16, 2010 21:08
Geometria Plana
-
- (UFRGS) Complexo
por flavio2010 » Sáb Jul 17, 2010 12:51
- 1 Respostas
- 2067 Exibições
- Última mensagem por Tom

Sáb Jul 17, 2010 14:10
Números Complexos
-
- Função UFRGS
 por Kelvin Brayan » Ter Mai 24, 2011 18:47
por Kelvin Brayan » Ter Mai 24, 2011 18:47
- 3 Respostas
- 7881 Exibições
- Última mensagem por Kelvin Brayan

Qua Mai 25, 2011 00:52
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 tem
tem e num mesmo sistema de coordenadas cartesianas ortogonais, pode-se verificar que o número de soluções da equação f(x) = g(x)é
e num mesmo sistema de coordenadas cartesianas ortogonais, pode-se verificar que o número de soluções da equação f(x) = g(x)é

 Raio = 1
Raio = 1 ![D = \ell\:\sqrt[]{2} D = \ell\:\sqrt[]{2}](/latexrender/pictures/777e9f39975a29b503809d772846b527.png) . Logo você percebe que a área do segundo quadrado é 2, do terceiro é 4, do quarto é 8, ... , caindo numa PG de razão 2. Usando a fórmula da soma de uma PG finita chega-se ao resultado de
. Logo você percebe que a área do segundo quadrado é 2, do terceiro é 4, do quarto é 8, ... , caindo numa PG de razão 2. Usando a fórmula da soma de uma PG finita chega-se ao resultado de 

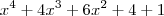 então é fácil perceber que:
então é fácil perceber que: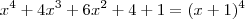
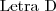 .
.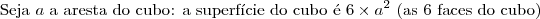
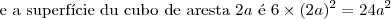


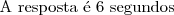



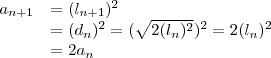

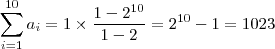
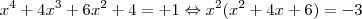
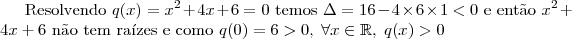
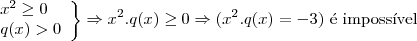

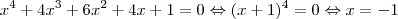
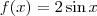 e
e 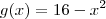 e num mesmo sistema de coordenadas cartesianas ortogonais, pode-se verificar que o número de soluções da equação f(x) = g(x)é
e num mesmo sistema de coordenadas cartesianas ortogonais, pode-se verificar que o número de soluções da equação f(x) = g(x)é![\phi(x)=x^2+2\sin{x}-16\\
\phi'(x)=2x+2\cos{x}\\
\phi''(x)=2-2\sin{x} \Rightarrow \forall x \in \mathbb{R},\;\phi''(x)\geq 0 \; \Rightarrow \phi' \text{ \'e crescente}\\
\left\!\!\!\!\begin{array}{r}\phi'\text{estr.crescente, continua sobre }[-\frac{\pi}{2};0]\\ \phi'(-\frac{\pi}{2})=-\pi\\ \phi'(0)=2 \end{array}\!\!\!\right\}\!\!\!\Rightarrow \!\!\exists\alpha\!\!\in ]\frac{-\pi}{2};0[\text{\'unico tal que }\phi'(\alpha)=0 \\
\phi \text{ decrescente em }]-\infty;\alpha]\text{ e crescente em }[\alpha;+\infty[\\
\phi'(\alpha)=0\Rightarrow \alpha=-\cos{\alpha}\Rightarrow \phi(\alpha)=\cos^2{\alpha}+2\sin{\alpha}-16=-\sin^2{\alpha}+2\sin{\alpha}-15\\
\text{Seja }t=\sin{\alpha}\text{ vemos que }-t^2+2t-15=0 \text{ n\~ao tem ra\'izes e } -t^2+2t-15<0\\
\text{ou seja }\phi(\alpha)<0 \phi(x)=x^2+2\sin{x}-16\\
\phi'(x)=2x+2\cos{x}\\
\phi''(x)=2-2\sin{x} \Rightarrow \forall x \in \mathbb{R},\;\phi''(x)\geq 0 \; \Rightarrow \phi' \text{ \'e crescente}\\
\left\!\!\!\!\begin{array}{r}\phi'\text{estr.crescente, continua sobre }[-\frac{\pi}{2};0]\\ \phi'(-\frac{\pi}{2})=-\pi\\ \phi'(0)=2 \end{array}\!\!\!\right\}\!\!\!\Rightarrow \!\!\exists\alpha\!\!\in ]\frac{-\pi}{2};0[\text{\'unico tal que }\phi'(\alpha)=0 \\
\phi \text{ decrescente em }]-\infty;\alpha]\text{ e crescente em }[\alpha;+\infty[\\
\phi'(\alpha)=0\Rightarrow \alpha=-\cos{\alpha}\Rightarrow \phi(\alpha)=\cos^2{\alpha}+2\sin{\alpha}-16=-\sin^2{\alpha}+2\sin{\alpha}-15\\
\text{Seja }t=\sin{\alpha}\text{ vemos que }-t^2+2t-15=0 \text{ n\~ao tem ra\'izes e } -t^2+2t-15<0\\
\text{ou seja }\phi(\alpha)<0](/latexrender/pictures/56cd4f5842222ffa3cf56bea01e2a9e4.png)
![\left \begin{array}{r}\phi\text{ continua sobre }\mathbb{R}\\
\phi\text{ estritamente decrescente sobre }]-\infty;\alpha[\\
\phi\text{ estritamente crescente sobre }]\alpha;+\infty[\\
\phi(-2\pi)>0 ,\phi(\alpha)<0,\phi(2\pi)>0 \end{array}\right \} \Rightarrow\left \{ \begin{array}{l}\exists x_1 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_1)=0\\
\exists x_2 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_2)=0\\
\forall x < -2\pi \text{ ou }x>2\pi,\;\phi(x)>0 \end{array}\right \left \begin{array}{r}\phi\text{ continua sobre }\mathbb{R}\\
\phi\text{ estritamente decrescente sobre }]-\infty;\alpha[\\
\phi\text{ estritamente crescente sobre }]\alpha;+\infty[\\
\phi(-2\pi)>0 ,\phi(\alpha)<0,\phi(2\pi)>0 \end{array}\right \} \Rightarrow\left \{ \begin{array}{l}\exists x_1 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_1)=0\\
\exists x_2 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_2)=0\\
\forall x < -2\pi \text{ ou }x>2\pi,\;\phi(x)>0 \end{array}\right](/latexrender/pictures/e541cc339277324141018ac2a21491d7.png)