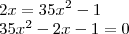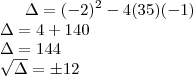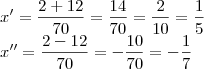por jamiel » Ter Mai 10, 2011 14:03
por jamiel » Ter Mai 10, 2011 14:03
Resolva as equações exponenciais.
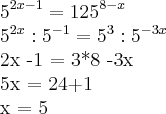
Acredito estar certa, mas se alguém puder fazer alguma análise!
=============================
![\sqrt[5]{{3}^{2x}}={2.187}^{\frac{{35x}^{2}-1}{35}}
{3}^{\frac{2x}{5}}=7*\frac{{35x}^{2}-1}{35} \sqrt[5]{{3}^{2x}}={2.187}^{\frac{{35x}^{2}-1}{35}}
{3}^{\frac{2x}{5}}=7*\frac{{35x}^{2}-1}{35}](/latexrender/pictures/faf317b98ffaeb2e05d768891fa32b24.png)
Sinceramente, nesta segunda equação, não consigo passar daí!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por carlosalesouza » Ter Mai 10, 2011 16:10
por carlosalesouza » Ter Mai 10, 2011 16:10
Na verdade, meu caro, tem um probleminha
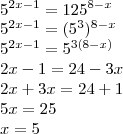
Note que
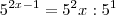
... o 1 é positivo, pois:
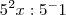
seria o mesmo que:
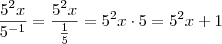
Ok?
Com a outra, vamos primeiro fatorar o 2.187, que fica igual a
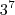
Agora:
![\\
\sqrt[5]{{3}^{2x}}={2.187}^{\frac{{35x}^{2}-1}{35}}\\
3^{\frac{2x}{5}}=3^7^{\frac{35x^2-1}{35}}\\
\frac{2x}{5}=7\cdot \frac{35x^2-1}{35}\\
\frac{2x}{5}=\frac{35x^2-1}{5} \\
\sqrt[5]{{3}^{2x}}={2.187}^{\frac{{35x}^{2}-1}{35}}\\
3^{\frac{2x}{5}}=3^7^{\frac{35x^2-1}{35}}\\
\frac{2x}{5}=7\cdot \frac{35x^2-1}{35}\\
\frac{2x}{5}=\frac{35x^2-1}{5}](/latexrender/pictures/4b702bafd63c83d08ec55896ef4be200.png)
Como ambos os lados apresentam o mesmo divisor:
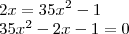
Aqui caímos temos uma equação de segundo grau:
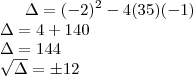
Assim:
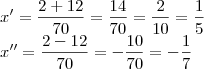
Ok?
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por jamiel » Qua Mai 11, 2011 00:30
por jamiel » Qua Mai 11, 2011 00:30
rsrsrsr O pior é q quando postei isso, logo em seguida consegui resolver, mas tive q sair e não postei a minha solução.
3^(2x/5)=(3^7)^(35x^(2)-1/35)
2x/5 = 7*35x^2-1/35
2x/5=1/5*35x^(2)-1
2x/5=35x^2/5 - 1/5
2x/5=7x^2 -1/5
-7x^2 + 2x/5 + 1/5
?144/25 = 12/5
' -1/7 e ''1/5
Mas valeu de qualquer forma, Carlos.
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação Exponencial - Problema 2
por jamiel » Seg Mai 09, 2011 18:58
- 7 Respostas
- 2964 Exibições
- Última mensagem por jamiel

Seg Mai 09, 2011 22:53
Sistemas de Equações
-
- Equação Exponencial - Problema 4
por jamiel » Sex Mai 13, 2011 03:00
- 7 Respostas
- 4066 Exibições
- Última mensagem por jamiel

Sex Mai 13, 2011 15:24
Sistemas de Equações
-
- Equação Exponencial - Problema 5
por jamiel » Sex Mai 13, 2011 15:42
- 7 Respostas
- 3736 Exibições
- Última mensagem por jamiel

Sex Mai 13, 2011 20:27
Sistemas de Equações
-
- Problema Com Inequação do Exponencial
por chenz » Sáb Jun 19, 2010 17:13
- 2 Respostas
- 1779 Exibições
- Última mensagem por chenz

Dom Jun 20, 2010 12:35
Funções
-
- Função Exponencial - problema 1
por jamiel » Sáb Mai 14, 2011 15:40
- 6 Respostas
- 2738 Exibições
- Última mensagem por jamiel

Dom Mai 15, 2011 10:40
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
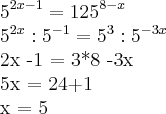
![\sqrt[5]{{3}^{2x}}={2.187}^{\frac{{35x}^{2}-1}{35}}
{3}^{\frac{2x}{5}}=7*\frac{{35x}^{2}-1}{35} \sqrt[5]{{3}^{2x}}={2.187}^{\frac{{35x}^{2}-1}{35}}
{3}^{\frac{2x}{5}}=7*\frac{{35x}^{2}-1}{35}](/latexrender/pictures/faf317b98ffaeb2e05d768891fa32b24.png)

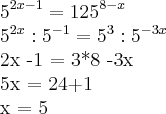
![\sqrt[5]{{3}^{2x}}={2.187}^{\frac{{35x}^{2}-1}{35}}
{3}^{\frac{2x}{5}}=7*\frac{{35x}^{2}-1}{35} \sqrt[5]{{3}^{2x}}={2.187}^{\frac{{35x}^{2}-1}{35}}
{3}^{\frac{2x}{5}}=7*\frac{{35x}^{2}-1}{35}](/latexrender/pictures/faf317b98ffaeb2e05d768891fa32b24.png)

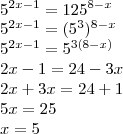
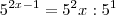 ... o 1 é positivo, pois:
... o 1 é positivo, pois: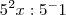
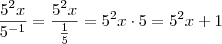
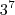
![\\
\sqrt[5]{{3}^{2x}}={2.187}^{\frac{{35x}^{2}-1}{35}}\\
3^{\frac{2x}{5}}=3^7^{\frac{35x^2-1}{35}}\\
\frac{2x}{5}=7\cdot \frac{35x^2-1}{35}\\
\frac{2x}{5}=\frac{35x^2-1}{5} \\
\sqrt[5]{{3}^{2x}}={2.187}^{\frac{{35x}^{2}-1}{35}}\\
3^{\frac{2x}{5}}=3^7^{\frac{35x^2-1}{35}}\\
\frac{2x}{5}=7\cdot \frac{35x^2-1}{35}\\
\frac{2x}{5}=\frac{35x^2-1}{5}](/latexrender/pictures/4b702bafd63c83d08ec55896ef4be200.png)