 por paula luna » Qui Mai 05, 2011 23:05
por paula luna » Qui Mai 05, 2011 23:05
paula luna escreveu:![\lim_{x\rightarrow 0} \left[ \frac{1}{x} -\frac{1}{\left|x \right|} \right] \lim_{x\rightarrow 0} \left[ \frac{1}{x} -\frac{1}{\left|x \right|} \right]](/latexrender/pictures/7d0789122ee03df44e03d007ab9d48db.png)
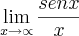
NOSSA NA VERDADE TEM UMAS 15 QUESTOES QUE EU NAO CONSIGO DE UMA LISTA DE UMAS 25 , MAS SE EU BOTAR TODAS VAO ME MANDAR A M... (COM RAZAO)
Obs.: Nao pode ser por grafico ¬¬... professor nao deixa (coisa boa ja que ele nao resolveu sequer um limite indeterminado pra saber como se faz)
Tu disse pra mim postar caso ainda tivesse duvida ... pois bem vi tuas aulas (as duas que tu recomendou e mais 2 outra) achei muito boas (parabens!) e ajudou a resolver aquele segundo limite (sen x / x x-->inf ) mas a outra eu ainda nao consegui.
Talvez nao tenha esclarecido minha duvida : estou com dificuldade por causa do modulo, eu sei conceito de modulo ... porem no limite eu nao tenho ideia de como fazer!
-
paula luna
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Mai 05, 2011 21:56
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Qui Mai 05, 2011 23:21
por LuizAquino » Qui Mai 05, 2011 23:21
Eu fico feliz que tenha gostado dos vídeos e que eles tenham lhe ajudado a resolver um dos exercícios.
Bem, vejamos o outro limite.
Primeiro, lembre-se que da definição de módulo temos que |x| = x, se x >= 0; |x| = -x, se x < 0.
Desse modo, vamos analisar o limite para x tendendo a 0 tanto pela esquerda quanto pela direita.
![\lim_{x\rightarrow 0^-} \left[ \frac{1}{x} -\frac{1}{|x|} \right] = \lim_{x\rightarrow 0^-} \left[ \frac{1}{x} -\frac{1}{-x}\right] = 2\lim_{x\rightarrow 0^-} \frac{1}{x} = -\infty \lim_{x\rightarrow 0^-} \left[ \frac{1}{x} -\frac{1}{|x|} \right] = \lim_{x\rightarrow 0^-} \left[ \frac{1}{x} -\frac{1}{-x}\right] = 2\lim_{x\rightarrow 0^-} \frac{1}{x} = -\infty](/latexrender/pictures/067b0cd69beeae18fa522b3e0d76916c.png)
![\lim_{x\rightarrow 0^+} \left[ \frac{1}{x} -\frac{1}{|x|} \right] = \lim_{x\rightarrow 0^+} \left[ \frac{1}{x} -\frac{1}{x}\right] = \lim_{x\rightarrow 0^-} 0 = 0 \lim_{x\rightarrow 0^+} \left[ \frac{1}{x} -\frac{1}{|x|} \right] = \lim_{x\rightarrow 0^+} \left[ \frac{1}{x} -\frac{1}{x}\right] = \lim_{x\rightarrow 0^-} 0 = 0](/latexrender/pictures/b2f3c0ba4a7cc2fe81820c0d516e95b4.png)
Como os limites laterais são diferentes, temos que o limite original não existe.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Dúvida ANOVA] Uma dúvida sobre a estatística correta
por gustamfar » Ter Mai 22, 2018 18:19
- 0 Respostas
- 11060 Exibições
- Última mensagem por gustamfar

Ter Mai 22, 2018 18:19
Estatística
-
- Dúvida PA
por Cleyson007 » Dom Jun 01, 2008 01:01
- 2 Respostas
- 10770 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:38
Progressões
-
- Dúvida
por miguelbaptista » Sex Jan 09, 2009 03:29
- 8 Respostas
- 12560 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:13
Logaritmos
-
- dúvida
por gdarius » Dom Ago 16, 2009 00:09
- 1 Respostas
- 3165 Exibições
- Última mensagem por Felipe Schucman

Dom Ago 16, 2009 02:35
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida!!
por GABRIELA » Qui Set 17, 2009 18:19
- 5 Respostas
- 5740 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:38
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

![\lim_{x\rightarrow 0} \left[ \frac{1}{x} -\frac{1}{\left|x \right|} \right] \lim_{x\rightarrow 0} \left[ \frac{1}{x} -\frac{1}{\left|x \right|} \right]](/latexrender/pictures/7d0789122ee03df44e03d007ab9d48db.png)
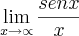

![\lim_{x\rightarrow 0^-} \left[ \frac{1}{x} -\frac{1}{|x|} \right] = \lim_{x\rightarrow 0^-} \left[ \frac{1}{x} -\frac{1}{-x}\right] = 2\lim_{x\rightarrow 0^-} \frac{1}{x} = -\infty \lim_{x\rightarrow 0^-} \left[ \frac{1}{x} -\frac{1}{|x|} \right] = \lim_{x\rightarrow 0^-} \left[ \frac{1}{x} -\frac{1}{-x}\right] = 2\lim_{x\rightarrow 0^-} \frac{1}{x} = -\infty](/latexrender/pictures/067b0cd69beeae18fa522b3e0d76916c.png)
![\lim_{x\rightarrow 0^+} \left[ \frac{1}{x} -\frac{1}{|x|} \right] = \lim_{x\rightarrow 0^+} \left[ \frac{1}{x} -\frac{1}{x}\right] = \lim_{x\rightarrow 0^-} 0 = 0 \lim_{x\rightarrow 0^+} \left[ \frac{1}{x} -\frac{1}{|x|} \right] = \lim_{x\rightarrow 0^+} \left[ \frac{1}{x} -\frac{1}{x}\right] = \lim_{x\rightarrow 0^-} 0 = 0](/latexrender/pictures/b2f3c0ba4a7cc2fe81820c0d516e95b4.png)

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
