Pense o seguinte.
O diametro da circunferencia é a diagonal do quadrado.
A diagonal dum quadrado de lado

é sempre
![\alpha\sqrt[]{2} \alpha\sqrt[]{2}](/latexrender/pictures/4fff6a7637f05449fed26931624c3004.png)
.
No seu caso. a diagonal é duas vezes o raio (diametro) entao fica que o lado do quadrado é
![\alpha\sqrt[]{2}} = 2\times8\sqrt[]{2} \alpha\sqrt[]{2}} = 2\times8\sqrt[]{2}](/latexrender/pictures/9bcff7fe80732bcb4801ce59ea1b33f7.png)
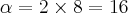
Dai voce percebe que seu quadrado tem lado 16.
Se voce quer a area da parte preta na figura. é simples
Area da circunferencia - area do quadrado = area desejada
Portanto:
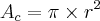
e

Ai voce faz a conta pans, só não vou falar muito pq acabei de me tocar que nao sei direito o que o problema pede, se for a area preta entao faça isso,
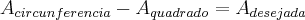
Mas de qualquer jeito, use aquela jogada da diagonal do quadrado ser sempre
![\alpha\sqrt[]{2} \alpha\sqrt[]{2}](/latexrender/pictures/4fff6a7637f05449fed26931624c3004.png)
. E do diametro ser a diagonal do quadrado. Saindo dai vc tem informação até demais
Espero ter ajudado, Abraço
![8 \sqrt[]{2} 8 \sqrt[]{2}](/latexrender/pictures/68ec525367b08678e151e9883e3334c9.png)
 --
-- ![r=8\sqrt[]{3} r=8\sqrt[]{3}](/latexrender/pictures/e963174c3c9c078bf1063cb489ebfd9f.png) --
-- 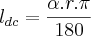
![{l}_{dc}= \frac{90.8\sqrt[]{2}.\pi}{180} {l}_{dc}= \frac{90.8\sqrt[]{2}.\pi}{180}](/latexrender/pictures/e9dc9a171ff8bc0ae0e4bc92e5be16c0.png) --
-- ![{l}_{dc}= 4\pi\sqrt[]{2} {l}_{dc}= 4\pi\sqrt[]{2}](/latexrender/pictures/9b840bdf4e4cda019f61e332b46aae01.png)
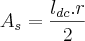 --
-- ![{A}_{s}= \frac{4\pi\sqrt[]{2}.8\sqrt[]{2}}{2} {A}_{s}= \frac{4\pi\sqrt[]{2}.8\sqrt[]{2}}{2}](/latexrender/pictures/6df638a8468d9af2759a4ae6836ef3e1.png) --
-- 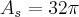


 é sempre
é sempre ![\alpha\sqrt[]{2} \alpha\sqrt[]{2}](/latexrender/pictures/4fff6a7637f05449fed26931624c3004.png) .
.![\alpha\sqrt[]{2}} = 2\times8\sqrt[]{2} \alpha\sqrt[]{2}} = 2\times8\sqrt[]{2}](/latexrender/pictures/9bcff7fe80732bcb4801ce59ea1b33f7.png)
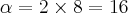
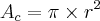

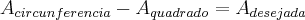


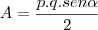
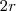 ,pois está inscrita em uma circunferência, e o ângulo entre elas é de
,pois está inscrita em uma circunferência, e o ângulo entre elas é de 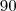 , desta forma temos,
, desta forma temos,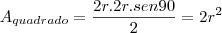
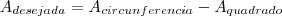


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.