01. Prove que se 0 < a < 1, entao:
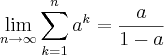 .
.e
02. Calcule
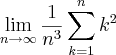 .
.Não soube resolver esses, mas consegui resolver o resto da lista toda... E me ocorreu que se eu conseguisse um modo de determinar os termos gerais de sequencias, sequencias que somam n termos nesses casos, eu conseguiria resolve-los mais facilmente. Basicamente é o que se pede no primeiro exercicio, certo. Mas o que eu imaginava era algo como, um termo geral em função de n que quando eu calculasse o limite desse termo geral tal que n tendesse ao infinito eu obteria o mesmo resultado da prova 01.
Acredito que tenha ficado pouco claro, vou tentar esclarecer um pouco mais
se eu tenho a sequencia (no caso da primeira) com n = 3 por exemplo. eu tenho os numeros: a, a², e a³... a soma a + a² + a³, se eu tiver n = 4 terei um termo a mais, em fim, se eu tivesse o termo geral para qualquer 'n' eu poderia calcular o limite com o n tendendo ao infinito e seria a mesma coisa que calcular o primeiro exercicio.
Bom, essa é a minha duvida, eu tentei pesquisar na internet nao obtive resultado (tbm por que minha duvida é dificil de ser colocada em palavras chave)
Muitíssimo obrigado!


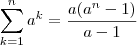 , com
, com 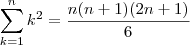 -- Nesse caso, há uma demonstração dessa identidade no apêndice sobre somatórios no livro de Cálculo de James Stewart.
-- Nesse caso, há uma demonstração dessa identidade no apêndice sobre somatórios no livro de Cálculo de James Stewart.