 por carlos_err » Sex Abr 29, 2011 20:32
por carlos_err » Sex Abr 29, 2011 20:32
Olá, estou com uma questão na minha lista que ñ estou conseguindo desenvolver a questão é:
Imprima gráficos das funções seno, cosseno, tangente, cotangente, secante e
cossecante, utilizando o Winplot.
Gostaria de saber pelo menos em exemplo de uma função que possa ser jogada no winplot.
-
carlos_err
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Abr 29, 2011 20:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por FilipeCaceres » Sex Abr 29, 2011 21:10
por FilipeCaceres » Sex Abr 29, 2011 21:10
Não sei bem o que vc gostaria, mas para plotar gráficos no winplot basta fazer o seguinte:
Exemplo:
Winplot>2-dim>Equações>1.Explícita
Digite a função, exemplo xsin(x).
Seria isto que vc gostaria de saber?
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por carlos_err » Sex Abr 29, 2011 21:12
por carlos_err » Sex Abr 29, 2011 21:12
isso msm, se eu quiser do cosseno,tangente....
é só ir alterando???
OBG!
-
carlos_err
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Abr 29, 2011 20:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por FilipeCaceres » Sex Abr 29, 2011 21:52
por FilipeCaceres » Sex Abr 29, 2011 21:52
Isto mesmo, é só escrever as funções
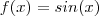

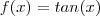
...
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por LuizAquino » Sex Abr 29, 2011 21:56
por LuizAquino » Sex Abr 29, 2011 21:56
Eu sei que a sua atividade pediu para usar o programa Winplot.
Entretanto, há um programa muito mais interessante do que o Winplot (em muitos aspectos), chamado de GeoGebra.
A página oficial do GeoGebra é:
http://www.geogebra.orgEu disponibilizei em meu canal no YouTube um curso sobre esse programa. O endereço é:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por carlos_err » Sex Abr 29, 2011 22:02
por carlos_err » Sex Abr 29, 2011 22:02
ok,
obg, dps vou verificar esses outro programas
-
carlos_err
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Abr 29, 2011 20:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda com funções
por Duhh » Qui Ago 19, 2010 22:17
- 5 Respostas
- 2693 Exibições
- Última mensagem por Douglasm

Sex Ago 20, 2010 10:39
Funções
-
- Ajuda - Funções
por _ITINHO_ » Qua Out 13, 2010 19:27
- 3 Respostas
- 4686 Exibições
- Última mensagem por MarceloFantini

Qui Out 14, 2010 16:16
Funções
-
- funçoes ajuda!!
por flavio970 » Seg Out 26, 2015 17:43
- 1 Respostas
- 1528 Exibições
- Última mensagem por nakagumahissao

Sáb Out 31, 2015 16:31
Funções
-
- funçoes ajuda!
por flavio970 » Seg Out 26, 2015 12:47
- 1 Respostas
- 1489 Exibições
- Última mensagem por nakagumahissao

Sex Nov 06, 2015 10:57
Funções
-
- Ajuda !! Funções !
por maymazzi » Sex Mar 11, 2016 22:39
- 0 Respostas
- 3411 Exibições
- Última mensagem por maymazzi

Sex Mar 11, 2016 22:39
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



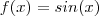

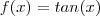

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)