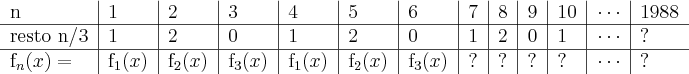por scorpion » Sáb Out 25, 2008 11:09
por scorpion » Sáb Out 25, 2008 11:09
Pessoal gostaria de uma ajuda neste problema:
Seja
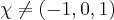
. Se
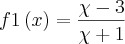
e
![fn+1\left( x\right)= f1\left[ fn\left( x\right)\right] fn+1\left( x\right)= f1\left[ fn\left( x\right)\right]](/latexrender/pictures/90881882bf57a1efa6d4ddb0c06e0cc4.png)
para todo n natural então
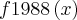
é :
resp:
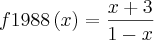
Eu fiz deste modo:
se n=1
![f2\left( x\right)=f1\left[ f1\left( x\right)\right] f2\left( x\right)=f1\left[ f1\left( x\right)\right]](/latexrender/pictures/074389d2b4baf29b1cf9acab436cd201.png)
.
Fiz desta forma até n=5, pois quando n=5 a função ficou igual a função de n=2.
O problema é que agora eu não sei como fazer para chegar em
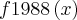
.
Não precisam resolver só me expliquem o que fazer.
Obrigado a todos.
-
scorpion
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Out 19, 2008 19:52
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por admin » Ter Out 28, 2008 22:02
por admin » Ter Out 28, 2008 22:02
Olá
scorpion, boas-vindas!
Como você bem percebeu ao fazer até

, ocorreu que

.
Sequencialmente em

a cada 3 percebemos que

.
Então, a sugestão é analisar os restos da divisão de

por 3.
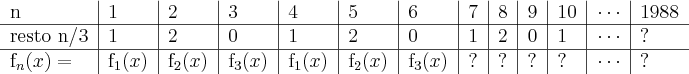
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por scorpion » Qua Out 29, 2008 14:26
por scorpion » Qua Out 29, 2008 14:26
Muito obrigado pela ajuda. Agora entendi como se faz.
Abraços.
-
scorpion
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Out 19, 2008 19:52
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função composta]Achar o dominio de uma função composta
por lucasmath » Dom Abr 12, 2015 16:09
- 0 Respostas
- 2234 Exibições
- Última mensagem por lucasmath

Dom Abr 12, 2015 16:09
Funções
-
- [FUNÇÃO] NAO CONSIGO ENTENDER FUNÇÃO COMPOSTA!
por Gabriela AlmeidaS » Seg Mai 12, 2014 19:18
- 5 Respostas
- 5466 Exibições
- Última mensagem por Toussantt

Dom Jan 24, 2016 15:34
Funções
-
- Função Composta
 por ginrj » Ter Jun 30, 2009 17:35
por ginrj » Ter Jun 30, 2009 17:35
- 4 Respostas
- 17049 Exibições
- Última mensagem por LuizAquino

Sáb Mar 03, 2012 14:34
Funções
-
- Função composta
 por matemalouco » Sáb Ago 15, 2009 20:43
por matemalouco » Sáb Ago 15, 2009 20:43
- 2 Respostas
- 3986 Exibições
- Última mensagem por Elcioschin

Seg Ago 17, 2009 10:26
Funções
-
- Função composta
por Maria_Santos » Qua Set 09, 2009 14:57
- 1 Respostas
- 1972 Exibições
- Última mensagem por Elcioschin

Qua Set 09, 2009 22:33
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
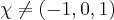 . Se
. Se 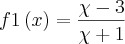
![fn+1\left( x\right)= f1\left[ fn\left( x\right)\right] fn+1\left( x\right)= f1\left[ fn\left( x\right)\right]](/latexrender/pictures/90881882bf57a1efa6d4ddb0c06e0cc4.png) para todo n natural então
para todo n natural então 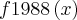 é :
é :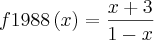
![f2\left( x\right)=f1\left[ f1\left( x\right)\right] f2\left( x\right)=f1\left[ f1\left( x\right)\right]](/latexrender/pictures/074389d2b4baf29b1cf9acab436cd201.png) .
.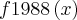 .
.

 , ocorreu que
, ocorreu que  .
. a cada 3 percebemos que
a cada 3 percebemos que  .
.