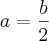ajudaaa

[willwgo]

como eu resolvo esse sistema:
(4a+2b+c=-8
(16a+4b+c=-64
(9a-3b+c=27

me ajudem ai eu nau entendo mto essa materia me digam como resolver este exercicio!
obrigado

[Molina]

Boa tarde.

Provavelmente você aprendeu alguns métodos na sala de aula para resolver sistemas lineares. Sabes me dizer quais? Eu não posso te passar uma resolução de um método que você não viu ainda...

Fico no aguardo!

[willwgo]

Eu nau me lembro pois estou estudando sozinho,para um concurso que eu vou fazer, se vc poder me ajudar ou ensinar ficarei mto agradecido!
mais o jeito q eu sei fazer e so o de (sistema linear de duas equaçõe e duas variaveis) assim:
(3x+2y=4
(6x+y=2

-2*(3x+2y=4
(6x+y=2

(-6x-4y=-8
(6x+y=2
-------------
-3y=-6
y=-6/-3
y=2; x=0

(assim é o jeito q eu sei fazer)
queria saber se tbm tem com resolver pelo metodo da Matriz?

[DanielRJ]

Voce pode resolver esse sistema por escalonamento ou equação matricial.
Te aconselho ir no youtube e dar uma estudada se alguem resolver voce não irá entender.

[carlosalesouza]

Meu caro,

É bem simples. Muita gente acha que matemática é decorar fórmulas e métodos. Isso é um equívoco, pra aprender ou mesmo pra resolver um problema matemático, você precisa usar o raciocínio.

Vamos estabelecer aqui algumas pressuposições mínimas e conseguiremos resolver esse problema e lembrar disso facilitará muitos outros.

O mais importante no sistema de equações é lembrar que igualdade é igualdade, ou seja, dois elementos ou grupos de elementos que estejam equacionados (sejam iguais) serão sempre iguais e podem ser substituídos um pelo outro e se forem afetados de forma equivalente, continuarão sendo iguais.

Por isso, lembre-se, quando você "passa" um valor para o "outro lado" de uma igualdade, o que você faz, na verdade, é modificar ambos os termos, de forma equivalente, eliminando de um deles um elemento que se queira remover e esse modificador será aplicado em ambos os lados

Como exemplo, se dizemos que , para sabermos quanto vale o , é necessário isolá-lo, ou seja, eliminar os elementos que o acompanham, neste caso, o 2 que o multiplica.

Para eliminar este 2, devemos submetê-lo a uma operação que o anule. De forma limplificada, podemos considerar como operações opostas:

multiplicação e divisão
adição e subtração
potência e radiciação

Estas operações realizadas em valores equivalentes os anulam. Assim, para anular o 2 que multiplica, dividimos por 2 os dois lados da igualdade.



Resultando em

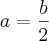
Aplique esta idéia em cada uma das linhas do sistema de equações e em cada uma delas substitua uma das variáveis, a, b ou c. Depois, substituindo as variáveis entre si, seguindo o princípio da igualdade e, com um pouco de raciocínio você vai descobrir as relações entre elas.

Lembre-se, num sistema de equações, as variáveis terão o mesmo valor em todas as suas linhas, ou seja, se voce descobrir, na primeira linha que a = 2b+3c ou qualquer outro valor, você poderá substitui-lo por 2b+3c em qualquer uma das outras expressões.

Espero ter ajudado e não confundido mais... rs

Um abraço

[Molina]

Como faz tempo que você não estuda o mais interessante é pegar algum livro (ou procurar na internet mesmo, como sugeriu o colega) tratando do assunto. Por que daí sim você irá entender o que estará fazendo...

Procure sobre Regra de Cramer.

[LuizAquino]

Eis um ótimo lugar para você revisar/aprender os conteúdos de Matemática do ensino fundamental ou médio:
http://www.youtube.com/nerckie

Nesse canal há inclusive aulas sobre sistema de equações lineares.

[willwgo]

obrigado a todos me ajudaram mto.!