![\lim_{x\rightarrow0}\frac{a\sqrt[3]{x+8}-b}{x}=\frac{1}{4} \lim_{x\rightarrow0}\frac{a\sqrt[3]{x+8}-b}{x}=\frac{1}{4}](/latexrender/pictures/471a55837924b1bd87965f937d53ba6a.png)
Determinar o valor das constantes a e b

![\lim_{x\rightarrow0}\frac{a\sqrt[3]{x+8}-b}{x}=\frac{1}{4} \lim_{x\rightarrow0}\frac{a\sqrt[3]{x+8}-b}{x}=\frac{1}{4}](/latexrender/pictures/471a55837924b1bd87965f937d53ba6a.png)

![\lim_{x\to 0} a\sqrt[3]{x+8}-b = 0 \lim_{x\to 0} a\sqrt[3]{x+8}-b = 0](/latexrender/pictures/1c4bb09ae50fe049026af7abdb7de75a.png) . Disso você deve obter que b = 2a.
. Disso você deve obter que b = 2a.![\lim_{x\to 0}\frac{a\sqrt[3]{x+8}-2a}{x}=\frac{1}{4} \lim_{x\to 0}\frac{a\sqrt[3]{x+8}-2a}{x}=\frac{1}{4}](/latexrender/pictures/f0f6d01bfc6b87f2e176f0f6e7d3c900.png) .
.![\lim_{x\to 0}\frac{\sqrt[3]{a^3(x+8)}-2a}{x}=\frac{1}{4} \lim_{x\to 0}\frac{\sqrt[3]{a^3(x+8)}-2a}{x}=\frac{1}{4}](/latexrender/pictures/14ef66eb5ed3d0d90de6710baa8c00c6.png) .
.![\left( \sqrt[3]{[a^3(x+8)]^2}+2a\sqrt[3]{a^3(x+8)} + 4a^2 \right) \left( \sqrt[3]{[a^3(x+8)]^2}+2a\sqrt[3]{a^3(x+8)} + 4a^2 \right)](/latexrender/pictures/4d9bf2bc3515757e005ea03062fa1ed9.png) . Em seguida, lembre-se do produto notável
. Em seguida, lembre-se do produto notável 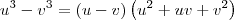 .
.
LuizAquino escreveu:multiplique tanto o numerador quanto o denominador por



![\lim_{x\to 0} a\sqrt[3]{x+8}-b = c \lim_{x\to 0} a\sqrt[3]{x+8}-b = c](/latexrender/pictures/5a257594061199ece2232769a00c5a6b.png) , com c uma constante não nula.
, com c uma constante não nula.![\lim_{x\to 0}\frac{a\sqrt[3]{x+8}-b}{x} = \left(\lim_{x\to 0}a\sqrt[3]{x+8}-b\right)\left(\lim_{x\to 0}\frac{1}{x}\right) = c \left(\lim_{x\to 0}\frac{1}{x}\right) \lim_{x\to 0}\frac{a\sqrt[3]{x+8}-b}{x} = \left(\lim_{x\to 0}a\sqrt[3]{x+8}-b\right)\left(\lim_{x\to 0}\frac{1}{x}\right) = c \left(\lim_{x\to 0}\frac{1}{x}\right)](/latexrender/pictures/dbae65bc80361eef4a91923312fe7ccb.png)
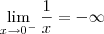
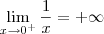
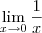 , já que os seus laterais são distintos.
, já que os seus laterais são distintos.

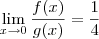 .
.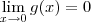 . Além disso, também sabemos que: g(x)<0, se x<0; g(x)>0, se x>0. Isso significa que
. Além disso, também sabemos que: g(x)<0, se x<0; g(x)>0, se x>0. Isso significa que 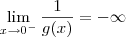 e
e 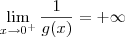 .
.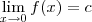 , com c uma constante não nula, então o limite
, com c uma constante não nula, então o limite 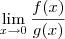 não existiria e portanto a equação original não seria válida.
não existiria e portanto a equação original não seria válida. .
.
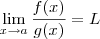 se forem uma indeterminação do tipo
se forem uma indeterminação do tipo  .
.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

