 por Thais_silva » Qui Abr 28, 2011 10:35
por Thais_silva » Qui Abr 28, 2011 10:35
-
Thais_silva
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Abr 28, 2011 09:25
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por FilipeCaceres » Qui Abr 28, 2011 11:18
por FilipeCaceres » Qui Abr 28, 2011 11:18
Observe que você errou nesta parte
x^2-x-16-4=0
x^2-x-12=0
Correto

Portanto,

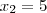
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- pode me ajudar
por johnny » Sex Out 22, 2010 17:59
- 3 Respostas
- 1970 Exibições
- Última mensagem por Neperiano

Seg Out 25, 2010 21:19
Cálculo: Limites, Derivadas e Integrais
-
- Alguem pode ajudar-me?
por carlos r m oliveira » Seg Out 05, 2009 11:35
- 1 Respostas
- 2552 Exibições
- Última mensagem por Neperiano

Dom Jul 03, 2011 21:05
Estatística
-
- Quem pode me ajudar?
por Livia Primo » Ter Fev 02, 2010 18:44
- 2 Respostas
- 4099 Exibições
- Última mensagem por Livia Primo

Qua Fev 03, 2010 22:22
Funções
-
- Alguém pode me ajudar?
por apoliveirarj » Seg Jul 19, 2010 18:20
- 1 Respostas
- 3393 Exibições
- Última mensagem por Douglasm

Seg Jul 19, 2010 18:49
Matemática Financeira
-
- Alguém pode me ajudar?
por Andromeda » Seg Set 19, 2011 20:19
- 2 Respostas
- 2421 Exibições
- Última mensagem por Andromeda

Seg Set 19, 2011 21:13
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
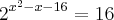
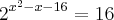
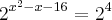
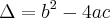
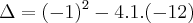
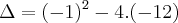
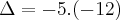
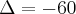
![x= \frac{-b\pm\sqrt[2]{\Delta}}{2a} x= \frac{-b\pm\sqrt[2]{\Delta}}{2a}](/latexrender/pictures/b71958bd94d49680e859b093b1adabe4.png)
![x=\frac{1\pm\sqrt[2]{60}}{2.1} x=\frac{1\pm\sqrt[2]{60}}{2.1}](/latexrender/pictures/6c273db16461dca43382687baa238551.png)
![x=\frac{1\pm\sqrt[2]{60}}{2} x=\frac{1\pm\sqrt[2]{60}}{2}](/latexrender/pictures/9475ae4e9879277be9111d56fffbe847.png)
![{x}_{1}=\frac{1+\sqrt[2]{60}}{2} = \frac{1+7,7}{2} = \frac{8,7}{2} = 4,35 {x}_{1}=\frac{1+\sqrt[2]{60}}{2} = \frac{1+7,7}{2} = \frac{8,7}{2} = 4,35](/latexrender/pictures/3baaf09126f04f53d4017ad8ca3f3f0d.png)
![{x}_{2}=\frac{1-\sqrt[2]{60}}{2} = \frac{1-7,7}{2} = \frac{6,7}{2} = 3,35 {x}_{2}=\frac{1-\sqrt[2]{60}}{2} = \frac{1-7,7}{2} = \frac{6,7}{2} = 3,35](/latexrender/pictures/bde0096cc1a04e785596a9a8ed0d94c1.png)

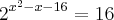
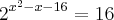
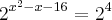
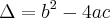
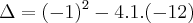
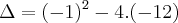
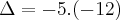
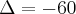
![x= \frac{-b\pm\sqrt[2]{\Delta}}{2a} x= \frac{-b\pm\sqrt[2]{\Delta}}{2a}](/latexrender/pictures/b71958bd94d49680e859b093b1adabe4.png)
![x=\frac{1\pm\sqrt[2]{60}}{2.1} x=\frac{1\pm\sqrt[2]{60}}{2.1}](/latexrender/pictures/6c273db16461dca43382687baa238551.png)
![x=\frac{1\pm\sqrt[2]{60}}{2} x=\frac{1\pm\sqrt[2]{60}}{2}](/latexrender/pictures/9475ae4e9879277be9111d56fffbe847.png)
![{x}_{1}=\frac{1+\sqrt[2]{60}}{2} = \frac{1+7,7}{2} = \frac{8,7}{2} = 4,35 {x}_{1}=\frac{1+\sqrt[2]{60}}{2} = \frac{1+7,7}{2} = \frac{8,7}{2} = 4,35](/latexrender/pictures/3baaf09126f04f53d4017ad8ca3f3f0d.png)
![{x}_{2}=\frac{1-\sqrt[2]{60}}{2} = \frac{1-7,7}{2} = \frac{6,7}{2} = 3,35 {x}_{2}=\frac{1-\sqrt[2]{60}}{2} = \frac{1-7,7}{2} = \frac{6,7}{2} = 3,35](/latexrender/pictures/bde0096cc1a04e785596a9a8ed0d94c1.png)

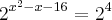
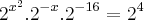
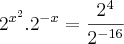
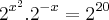
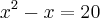
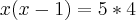 (Isolei x no primeiro membro e fatorei 20)
(Isolei x no primeiro membro e fatorei 20)


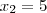

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.