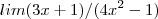

Não consegui escrever pelo Latex, mas x tende a (1/2) pela esquerda
Preciso calcular esse limite de forma que não haja indefinação (divisão por zero). Já tentei fatorar por x mas não dá certo.
Obrigada pela ajuda.

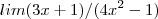



[tex]\lim_{x \to \frac{1}{2}^-}\frac{3x + 1}{4x^2 - 1}[/tex]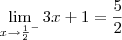 .
.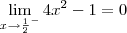 . Além disso, analisando o sinal da função
. Além disso, analisando o sinal da função 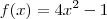 , sabemos que f(x)<0 se -1/2 < x < 1/2. Ou seja, para valores de x próximos a 1/2 pela esquerda, temos que f(x)<0.
, sabemos que f(x)<0 se -1/2 < x < 1/2. Ou seja, para valores de x próximos a 1/2 pela esquerda, temos que f(x)<0.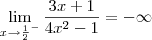


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes