 por Kelvin Brayan » Dom Abr 24, 2011 20:36
por Kelvin Brayan » Dom Abr 24, 2011 20:36
Sabendo-se que 302 400 = 64x27x25x7, pode-se concluir que o número de divisores de 302 400, que são múltiplos de 6, é igual a?
Eu já achei que 302 400 tem 168 divisores, mas como faço para descobrir o número de divisores múltiplos de 6 ?

-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por LuizAquino » Dom Abr 24, 2011 21:07
por LuizAquino » Dom Abr 24, 2011 21:07
mas como faço para descobrir o número de divisores múltiplos de 6 ?

Para que um número seja múltiplo de 6 ele deve ser múltiplo de 2 e 3 ao mesmo tempo.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Kelvin Brayan » Dom Abr 24, 2011 23:03
por Kelvin Brayan » Dom Abr 24, 2011 23:03
Tudo bem... mas qual é o procedimento que devo tomar para descobrir a quantidade de números divisores de 302 400 e múltiplos de 6 ? Como vou descobrir isso?
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por LuizAquino » Dom Abr 24, 2011 23:26
por LuizAquino » Dom Abr 24, 2011 23:26
Assim como foi feito no tópico [1], você pode determinar quantos são os divisores que não são múltiplos de 6. Em seguida, basta subtrair o total de divisores pelo total de divisores que não são múltiplos de 6.
Referência
[1]
Questão UFV-MG -
viewtopic.php?f=106&t=4513
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Kelvin Brayan » Seg Abr 25, 2011 01:06
por Kelvin Brayan » Seg Abr 25, 2011 01:06
Desculpem-me pela ignorância, mas será que alguém poderia resolver essa questão para mim ? Assim, eu poderia ver como se faz. Estou "enroscado" ainda somente nessa questão.
Obrigado !
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por LuizAquino » Seg Abr 25, 2011 10:26
por LuizAquino » Seg Abr 25, 2011 10:26
Sabemos que

.
Como eu havia sugerido, vejamos quantos são os divisores que
não são múltiplos de 6.
Para que o divisor não seja múltiplo de 6, os fatores

e
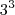
não podem aparecer ao mesmo tempo.
Desse modo, queremos saber quantos são os divisores formados por:
-
 -- teremos (2+1)(1+1) = 6 divisores.
-- teremos (2+1)(1+1) = 6 divisores. -
 -- teremos 6(2+1)(1+1) = 36 divisores. Note que no fator
-- teremos 6(2+1)(1+1) = 36 divisores. Note que no fator  nós não podemos contabilizar a possibilidade
nós não podemos contabilizar a possibilidade  , por esse motivo usamos 6 ao invés de (6+1).
, por esse motivo usamos 6 ao invés de (6+1). -
 -- teremos 3(2+1)(1+1) = 18 divisores. Novamente, nós não podemos contabilizar a possibilidade
-- teremos 3(2+1)(1+1) = 18 divisores. Novamente, nós não podemos contabilizar a possibilidade  , por esse motivo usamos 3 ao invés de (3+1).
, por esse motivo usamos 3 ao invés de (3+1).
Total de divisores que não são múltiplos de 6: 6 + 36 + 18 = 60.
Total de divisores: (6+1)(3+1)(2+1)(1+1) = 168.
Total de divisores que são múltiplos de 6: 168 - 60 = 108.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Kelvin Brayan » Seg Abr 25, 2011 10:54
por Kelvin Brayan » Seg Abr 25, 2011 10:54
Ouu valeu mesmo ein!
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12994 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- Questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:21
- 2 Respostas
- 10974 Exibições
- Última mensagem por Elcioschin

Ter Ago 18, 2009 08:54
Progressões
-
- QUESTÃO
por GABRIELA » Ter Set 08, 2009 16:32
- 2 Respostas
- 15116 Exibições
- Última mensagem por GABRIELA

Ter Set 08, 2009 21:21
Matrizes e Determinantes
-
- Questão da FCC
por wanderlymarques » Qua Nov 18, 2009 12:44
- 2 Respostas
- 5033 Exibições
- Última mensagem por wanderlymarques

Qui Nov 19, 2009 12:58
Cálculo: Limites, Derivadas e Integrais
-
- questão
por sirle ignes » Seg Mar 08, 2010 23:46
- 2 Respostas
- 4803 Exibições
- Última mensagem por sirle ignes

Ter Mar 09, 2010 17:32
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.








 .
. e
e 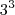 não podem aparecer ao mesmo tempo.
não podem aparecer ao mesmo tempo. -- teremos (2+1)(1+1) = 6 divisores.
-- teremos (2+1)(1+1) = 6 divisores. -- teremos 6(2+1)(1+1) = 36 divisores. Note que no fator
-- teremos 6(2+1)(1+1) = 36 divisores. Note que no fator  nós não podemos contabilizar a possibilidade
nós não podemos contabilizar a possibilidade  , por esse motivo usamos 6 ao invés de (6+1).
, por esse motivo usamos 6 ao invés de (6+1). -- teremos 3(2+1)(1+1) = 18 divisores. Novamente, nós não podemos contabilizar a possibilidade
-- teremos 3(2+1)(1+1) = 18 divisores. Novamente, nós não podemos contabilizar a possibilidade  , por esse motivo usamos 3 ao invés de (3+1).
, por esse motivo usamos 3 ao invés de (3+1).






