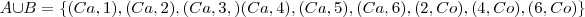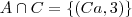Uma moeda e um dado são lançados. Temos U={(k,1),...(k,6),(c,1),...(c,6)} descreva os eventos:
a) A: ocorrer cara. Resposta: n(U)=6 U={(Ca,1), (Ca,2), (Ca,3,) (Ca,4), (Ca,5), (Ca,6)}.
b) B: ocorrer numero par. Resposta: n(U)=6 U={(2,Ca), (4,Ca),(6,Ca),(2,Co),(4,Co),(6,Co)}
c) C: ocorrer o numero 3
d) A u B
e) B ? C
f) A ? C
Poderiam me ajudar a responder a d), e) e f)? Me ajudando com uma já esta ótimo, só quero aprender direito esse negocio.