 por Kelvin Brayan » Dom Abr 24, 2011 11:01
por Kelvin Brayan » Dom Abr 24, 2011 11:01
Olá amigos, estava tentando resolver a questão abaixo, porém ela parece ser difícil e não sei muito bem o que devo fazer para resolvê-la. Como posso resolvê-la, descobrindo o discriminante ou realizando o método da soma e produto das raízes? De toda forma, parece complicado para mim.
(FEI-SP) Uma das raízes da equação x²-x-a = 0 é também raiz da equação x²+x-(a+20) = 0. Qual é o valor de a?

-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por NMiguel » Dom Abr 24, 2011 11:20
por NMiguel » Dom Abr 24, 2011 11:20
Consideremos
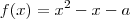
e
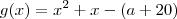
.
Sabemos que

e

têm um zero em comum.
Vamos então procurar o valor desse zero fazendo

.
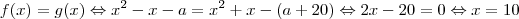
Se

é o único ponto em comum das duas funções, então só pode ser o zero comum.
Assim, sabemos que

-
NMiguel
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Ter Abr 19, 2011 17:09
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
-
 por Kelvin Brayan » Dom Abr 24, 2011 15:01
por Kelvin Brayan » Dom Abr 24, 2011 15:01
Nossa ! valeu cara !
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Uma questao complicada pra mim ;/
por hian » Dom Nov 14, 2010 16:50
- 1 Respostas
- 1627 Exibições
- Última mensagem por VtinxD

Seg Nov 15, 2010 01:33
Binômio de Newton
-
- [questão complicada]
por JKS » Qui Jun 20, 2013 01:48
- 1 Respostas
- 2458 Exibições
- Última mensagem por adauto martins

Seg Jan 05, 2015 16:24
Números Complexos
-
- Questão complicada de volume.
por ravi » Qui Set 19, 2013 15:36
- 1 Respostas
- 1720 Exibições
- Última mensagem por young_jedi

Sex Set 20, 2013 21:39
Cálculo: Limites, Derivadas e Integrais
-
- Função implícita; Questão complicada!
por jemourafer » Qui Mai 17, 2012 18:30
- 4 Respostas
- 4246 Exibições
- Última mensagem por Fabio Wanderley

Sáb Mai 19, 2012 03:16
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] complicada
por fabriel » Sáb Nov 02, 2013 12:47
- 3 Respostas
- 2018 Exibições
- Última mensagem por e8group

Sáb Nov 02, 2013 19:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




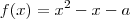 e
e 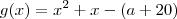 .
. e
e  têm um zero em comum.
têm um zero em comum. .
.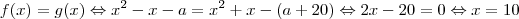
 é o único ponto em comum das duas funções, então só pode ser o zero comum.
é o único ponto em comum das duas funções, então só pode ser o zero comum.

