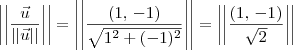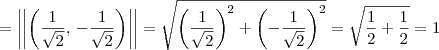por PatyMCastro » Qua Abr 20, 2011 14:47
por PatyMCastro » Qua Abr 20, 2011 14:47
OI, estou com duvida se devo colocar toda a equação na raiz quadrada, fiz da seguinte maneira ( e não deu o resultado correto que é 1):sendo u = (1,-1)
![\left|\frac{u}{\left|u \right|} \right| = \frac{(1,-1)}{\sqrt[2]{{1}^{2}({-1})^{2}}} = \frac{(1,-1)}{2} \left|\frac{u}{\left|u \right|} \right| = \frac{(1,-1)}{\sqrt[2]{{1}^{2}({-1})^{2}}} = \frac{(1,-1)}{2}](/latexrender/pictures/c36c54c53822da000aebe1a07cde4501.png)
como finalizo esta conta? o que fiz esta certo?
-
PatyMCastro
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Abr 20, 2011 14:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Qua Abr 20, 2011 15:38
por LuizAquino » Qua Abr 20, 2011 15:38
Qual é exatamente o texto do exercício?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por PatyMCastro » Qua Abr 20, 2011 15:54
por PatyMCastro » Qua Abr 20, 2011 15:54
Diz Assim: Dados os vetores u=(1,-1) , v= (-3,4) e w=(8,-6), calcular:
-
PatyMCastro
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Abr 20, 2011 14:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por PatyMCastro » Qua Abr 20, 2011 18:19
por PatyMCastro » Qua Abr 20, 2011 18:19
não, é só isso mesmo. Depois ele já dá o valor pra calcular. Esse é a letra h do Exercicio 16, pág 41 do Livro de Vetores e Geometria Analitica de Paulo Winterle.
-
PatyMCastro
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Abr 20, 2011 14:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Qua Abr 20, 2011 19:53
por LuizAquino » Qua Abr 20, 2011 19:53
Dado um vetor
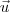
não nulo, sabemos que o vetor

tem módulo 1. Chamamos esse último vetor de
versor de
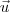
.
ExemploSeja
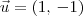
.
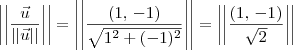
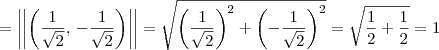
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por PatyMCastro » Qua Abr 27, 2011 00:34
por PatyMCastro » Qua Abr 27, 2011 00:34
Oi Luiz, Obrigada pela sua ajuda, me salvou a pele... desculpe por não ter agradecido antes... valeu mesmo !!
-
PatyMCastro
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Abr 20, 2011 14:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Módulo do Vetor
por Ana_Bela » Sáb Dez 13, 2014 22:51
- 2 Respostas
- 1859 Exibições
- Última mensagem por Ana_Bela

Dom Dez 14, 2014 12:26
Geometria Analítica
-
- [geometria analítica e calculo vetorial] modulo de um vetor
por Suellem Albuquerque » Sex Mar 28, 2014 15:36
- 0 Respostas
- 1176 Exibições
- Última mensagem por Suellem Albuquerque

Sex Mar 28, 2014 15:36
Geometria Analítica
-
- Duvida de módulo..
por priscila1992 » Dom Fev 12, 2012 00:10
- 1 Respostas
- 1067 Exibições
- Última mensagem por fraol

Dom Fev 12, 2012 00:37
Funções
-
- APLICAÇÃO DE DERIVADA! duvida em questão
por Mariteo » Qua Mar 01, 2017 17:14
- 0 Respostas
- 2919 Exibições
- Última mensagem por Mariteo

Qua Mar 01, 2017 17:14
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida em vetor
por elis81 » Qui Abr 15, 2010 20:20
- 3 Respostas
- 2659 Exibições
- Última mensagem por Mathmatematica

Dom Jun 13, 2010 01:41
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\left|\frac{u}{\left|u \right|} \right| = \frac{(1,-1)}{\sqrt[2]{{1}^{2}({-1})^{2}}} = \frac{(1,-1)}{2} \left|\frac{u}{\left|u \right|} \right| = \frac{(1,-1)}{\sqrt[2]{{1}^{2}({-1})^{2}}} = \frac{(1,-1)}{2}](/latexrender/pictures/c36c54c53822da000aebe1a07cde4501.png)

![\left|\frac{u}{\left|u \right|} \right| = \frac{(1,-1)}{\sqrt[2]{{1}^{2}({-1})^{2}}} = \frac{(1,-1)}{2} \left|\frac{u}{\left|u \right|} \right| = \frac{(1,-1)}{\sqrt[2]{{1}^{2}({-1})^{2}}} = \frac{(1,-1)}{2}](/latexrender/pictures/c36c54c53822da000aebe1a07cde4501.png)






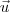 não nulo, sabemos que o vetor
não nulo, sabemos que o vetor  tem módulo 1. Chamamos esse último vetor de versor de
tem módulo 1. Chamamos esse último vetor de versor de 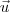 .
.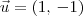 .
.