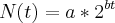 representa o crescimento de uma pop de bacterias. Neste caso, N(t) é o numero de bacterias no instante t (com t em horas) e a e b são constantes reais. Sabendo-se que no inicio da observação havia 3000 bacterias e que apos duas horas havia 4800 bacterias, determine:
representa o crescimento de uma pop de bacterias. Neste caso, N(t) é o numero de bacterias no instante t (com t em horas) e a e b são constantes reais. Sabendo-se que no inicio da observação havia 3000 bacterias e que apos duas horas havia 4800 bacterias, determine:a) os valores das constantes a e b
b) o numero de bacterias existentes apos meia hora
c) o tempo minimo necessario para que o numero de bacterias seja maior que 3 milhões


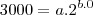
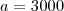
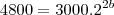
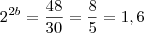
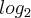 dos dois lados temos,
dos dois lados temos,

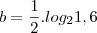
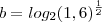
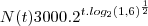
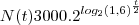
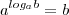
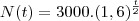

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)