 por paulacorreia » Qua Abr 13, 2011 23:33
por paulacorreia » Qua Abr 13, 2011 23:33
EQUAÇÕES BINÔMIAS:
nao to conseguindo resolver essa: x²-i=0
-
paulacorreia
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Abr 13, 2011 23:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
 por FilipeCaceres » Qua Abr 13, 2011 23:51
por FilipeCaceres » Qua Abr 13, 2011 23:51
Dica: Use 2º lei de Moivre.
Podemos reescreva a equação
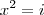
Para

Qualquer coisa poste novamente.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por paulacorreia » Qui Abr 14, 2011 20:48
por paulacorreia » Qui Abr 14, 2011 20:48
ela está reeescrita, mas ta respondida..?
-
paulacorreia
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Abr 13, 2011 23:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
 por FilipeCaceres » Qui Abr 14, 2011 21:00
por FilipeCaceres » Qui Abr 14, 2011 21:00
Não!!!
Eu só mudei a forma de escrita.
A dica é usar a 2º Fórmula de Moivre.
Acho que não adianta eu postar a solução, lhe dei uma dica agora você tente resolver, caso trave em algum lugar poste ate onde vc conseguiu que nós lhe ajudaremos.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equaçoes com Números Complexos -URGENTE
por Rose » Sex Nov 04, 2011 12:16
- 2 Respostas
- 1867 Exibições
- Última mensagem por Rose

Dom Nov 06, 2011 17:22
Números Complexos
-
- Números complexos módulo de dois números complexos important
por elisamaria » Qui Jun 11, 2015 16:56
- 1 Respostas
- 17117 Exibições
- Última mensagem por nakagumahissao

Qui Jun 11, 2015 19:20
Números Complexos
-
- Numeros complexos!
por Estela » Seg Mar 17, 2008 00:57
- 7 Respostas
- 13355 Exibições
- Última mensagem por andegledson

Seg Nov 02, 2009 21:41
Números Complexos
-
- Números Complexos
por michelle » Dom Ago 31, 2008 15:35
- 3 Respostas
- 10333 Exibições
- Última mensagem por admin

Dom Ago 31, 2008 21:00
Números Complexos
-
- Números Complexos
por Cleyson007 » Qui Mai 14, 2009 13:57
- 7 Respostas
- 13956 Exibições
- Última mensagem por Cleyson007

Sáb Mai 16, 2009 11:04
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



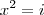




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.