 por Fabricio dalla » Qui Abr 07, 2011 01:56
por Fabricio dalla » Qui Abr 07, 2011 01:56
quando se tem uma funçao exponencial exp
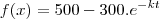
assim como toda funçao exponencial chega um determinado momento que ela passa a ser constante ou seja f(x) passa a assumir um unico valor,logo como que faço para calcular apartir de que momento ela passa a ser constante ?
desde ja agradeço.
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Neperiano » Qui Abr 07, 2011 09:50
por Neperiano » Qui Abr 07, 2011 09:50
Ola
Perai cuidado com isto que voce falou, ela não passa a ser constante, o que acontece é que como ele começa a fica cada vez mais perto do o, dá a impressão que é constante.
Para voce achar este ponto, ou monta o gráfico, ou acho que deve usar limite.
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Qui Abr 07, 2011 19:06
por MarceloFantini » Qui Abr 07, 2011 19:06
Uma função exponencial
NUNCA é constante. O que pode acontecer é que o seu
LIMITE pode ser zero, ou seja, quanto maiores os valores da variável, mais ela se aproxima do zero. No seu caso, não existe valor fixo: fazendo
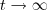
,
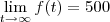
.
A propósito, cuidado pois a função é de t e não de x. Arrume seu latex.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida teórica.
por neilendrigo » Sex Mai 16, 2008 23:55
- 2 Respostas
- 2784 Exibições
- Última mensagem por neilendrigo

Sáb Mai 17, 2008 13:16
Geometria Plana
-
- [limites] - dúvida teórica
por natanaelskt » Qua Jul 16, 2014 02:04
- 2 Respostas
- 1882 Exibições
- Última mensagem por natanaelskt

Qui Jul 17, 2014 01:27
Cálculo: Limites, Derivadas e Integrais
-
- [integração por partes] Dúvida teórica
por natanaelskt » Qui Jul 17, 2014 03:00
- 1 Respostas
- 1568 Exibições
- Última mensagem por e8group

Qui Jul 17, 2014 10:03
Cálculo: Limites, Derivadas e Integrais
-
- [Estruturas Algébricas] Subconjuntos - Dúvida Teórica
por Pessoa Estranha » Seg Mar 10, 2014 19:51
- 1 Respostas
- 1560 Exibições
- Última mensagem por adauto martins

Sáb Dez 06, 2014 13:10
Álgebra Elementar
-
- Função Exponencial - Dúvida na resolução!
por jamiel » Dom Mai 15, 2011 14:09
- 1 Respostas
- 4779 Exibições
- Última mensagem por Claudin

Dom Mai 15, 2011 14:21
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

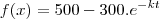


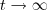 ,
, 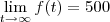 .
.
