eu já olhei alguns tópicos de espaço e subspaço vetorial (que me ajudaram mto) mas mesmo assim estou tendo dificuldade com um exercício que envolve números complexos... não sei como verificar os axiomas por causa da parte imaginária. :(
o exercício é o seguinte:
Seja V= {(x,y)| x,y
 C}. Mostre que V é um espaço vetorial sobre R com a adição e multiplicação por escalares definida como:
C}. Mostre que V é um espaço vetorial sobre R com a adição e multiplicação por escalares definida como:I) (x1, y1) + (x2,y2) = (x1+x2, y1+y2),
 (x1,y1) e (x2,y2)
(x1,y1) e (x2,y2)  V;
V;II) a (x,y) = (ax, ay),
 a
a  R e
R e  (x, y)
(x, y)  V.
V.Obrigada.


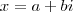 e
e 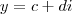 (onde
(onde 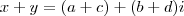 . Já o produto kx (com k um escalar), definimos como
. Já o produto kx (com k um escalar), definimos como 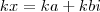 .
.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.