 por andersontricordiano » Qui Mar 31, 2011 02:19
por andersontricordiano » Qui Mar 31, 2011 02:19
Seja 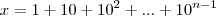 e
e 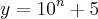
.
Determine ![\sqrt[]{xy+1} \sqrt[]{xy+1}](/latexrender/pictures/2881883fd200a2ae793f767ffea7993a.png)
Resposta:
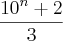
Por favor me ajudem!
Obrigado quem me ajudar!
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Qui Mar 31, 2011 12:32
por LuizAquino » Qui Mar 31, 2011 12:32
DicaNote que x representa soma dos n termos da p.g.
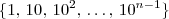
. Usando a fórmula para a
soma dos n termos de uma p.g., teremos que:
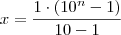
Agora, tente resolver o exercício.
Se tiver dificuldade, envie toda a resolução que você tentou fazer e onde está a sua dúvida.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por andersontricordiano » Qui Mar 31, 2011 16:03
por andersontricordiano » Qui Mar 31, 2011 16:03
Eu cheguei a esse calculo
![\sqrt[]{\frac{{10}^{n2}+(5*{10}^{n})-(1*{10}^{n})-5}{9}} \sqrt[]{\frac{{10}^{n2}+(5*{10}^{n})-(1*{10}^{n})-5}{9}}](/latexrender/pictures/dc1027633ae011598792cbe438d62993.png)
A minha dúvida é como se procede para calcular isso

Obrigado pela ajuda!
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Qui Mar 31, 2011 17:35
por FilipeCaceres » Qui Mar 31, 2011 17:35
Dando continuidade,
![\sqrt[]{\frac{{10}^{n2}+(5*{10}^{n})-(1*{10}^{n})-5}{9}+1} \sqrt[]{\frac{{10}^{n2}+(5*{10}^{n})-(1*{10}^{n})-5}{9}+1}](/latexrender/pictures/07f086cd959709fe0c4eab514f2871e7.png)
OBS.: esqueceu do +1
Arrumando temos,
![\sqrt[]{\frac{{10}^{2n}+4.{10}^{n}+4}{9}} \sqrt[]{\frac{{10}^{2n}+4.{10}^{n}+4}{9}}](/latexrender/pictures/f8d01c066248e9b3ec34172176fb78c8.png)
Observe que:
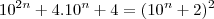
Assim temos,
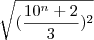
Portanto,
![\sqrt[]{xy+1}=\frac{10^n+2}{3} \sqrt[]{xy+1}=\frac{10^n+2}{3}](/latexrender/pictures/2bc36b36f51e7c54f674e3a59edc7d8b.png)
Espero ter ajudado.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo que envolve PA e PG
por andersontricordiano » Qua Mar 16, 2011 12:21
- 1 Respostas
- 2219 Exibições
- Última mensagem por Molina

Qua Mar 16, 2011 14:05
Progressões
-
- Calculo que envolve Sistemas Escalonados
por andersontricordiano » Sex Set 16, 2011 20:47
- 1 Respostas
- 1584 Exibições
- Última mensagem por MarceloFantini

Sex Set 16, 2011 20:58
Matrizes e Determinantes
-
- Calculo que envolve sistema lineares
por andersontricordiano » Sex Nov 04, 2011 19:15
- 1 Respostas
- 3487 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 31, 2012 18:55
Matrizes e Determinantes
-
- Cálculo A (engenharia) envolve Catenária e função sigmoidal
 por hericlisr » Sex Jun 19, 2015 01:34
por hericlisr » Sex Jun 19, 2015 01:34
- 0 Respostas
- 0 Exibições
- Última mensagem por Visitante

Qua Dez 31, 1969 22:00
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo A (engenharia) envolve Catenária e função sigmoidal
 por hericlisr » Qua Jun 17, 2015 16:35
por hericlisr » Qua Jun 17, 2015 16:35
- 0 Respostas
- 0 Exibições
- Última mensagem por Visitante

Qua Dez 31, 1969 22:00
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
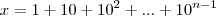 e
e 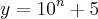 . Determine
. Determine ![\sqrt[]{xy+1} \sqrt[]{xy+1}](/latexrender/pictures/2881883fd200a2ae793f767ffea7993a.png)
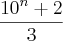

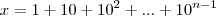 e
e 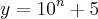 . Determine
. Determine ![\sqrt[]{xy+1} \sqrt[]{xy+1}](/latexrender/pictures/2881883fd200a2ae793f767ffea7993a.png)
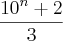

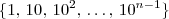 . Usando a fórmula para a soma dos n termos de uma p.g., teremos que:
. Usando a fórmula para a soma dos n termos de uma p.g., teremos que: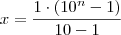

![\sqrt[]{\frac{{10}^{n2}+(5*{10}^{n})-(1*{10}^{n})-5}{9}} \sqrt[]{\frac{{10}^{n2}+(5*{10}^{n})-(1*{10}^{n})-5}{9}}](/latexrender/pictures/dc1027633ae011598792cbe438d62993.png)


![\sqrt[]{\frac{{10}^{n2}+(5*{10}^{n})-(1*{10}^{n})-5}{9}+1} \sqrt[]{\frac{{10}^{n2}+(5*{10}^{n})-(1*{10}^{n})-5}{9}+1}](/latexrender/pictures/07f086cd959709fe0c4eab514f2871e7.png) OBS.: esqueceu do +1
OBS.: esqueceu do +1![\sqrt[]{\frac{{10}^{2n}+4.{10}^{n}+4}{9}} \sqrt[]{\frac{{10}^{2n}+4.{10}^{n}+4}{9}}](/latexrender/pictures/f8d01c066248e9b3ec34172176fb78c8.png)
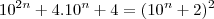
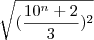
![\sqrt[]{xy+1}=\frac{10^n+2}{3} \sqrt[]{xy+1}=\frac{10^n+2}{3}](/latexrender/pictures/2bc36b36f51e7c54f674e3a59edc7d8b.png)
