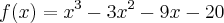Acho que a função que você quis passar é a seguinte:
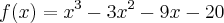
Vou dar apenas dicas de como resolver.
Caso mesmo assim você continue com dúvidas, deixe um comentário que eu auxilio novamente.
a) Para saber onde a função é crescente ou decrescente, usa-se a primeira derivada, ou seja, no intervalo em que:
f'(x) < 0 temos que f é decrescente, e
f'(x) > 0 temos que f é crescente.
b) Para saber pontos de máximo e mínimo utiliza-se f'(x) = 0. As raízes deste função (digamos que sejam
a e
b) você calcula a f''(a) e a f''(b).
Se essas segundas derivadas derem maior que zero entao f tem um
mínimo local em a ou b (dependendo de qual for maior que zero).
Se essas segundas derivadas derem menor que zero entao f tem um
máximo local em a ou b (dependendo de qual for menor que zero).
Qualquer dúvida, estamos a ordem!

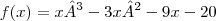 .Determine:
.Determine:
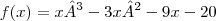 .Determine:
.Determine: