, com c sendo uma constante real,e A(t) medindo em kg.Se apos tres horas,a quantidade de açucar restante era de 10kg,quanto tempo será necessario para que restem 5kg de açucar?Dados:use as aproximaçoes Ln(0,4)=-0,92 e LN(0,2)=-1,61até onde fui
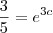
e que
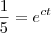
dai elevei ao cubo os 2 menbros da equaçao
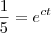
e substitui e fico assim:
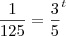
aquele t ali e da fraçao (3/5)
elevado a t
ai morri aqui :(
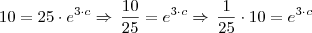
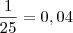e multiplicado por 10 resulta em 0,4 e então poderemos aplicar o Ln em ambos os lados da igualdade para obtermos o valor de c: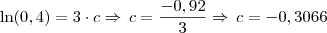
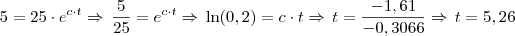
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)