_______________________________________________________________________________________________________________________________________
1ª) Um cidadão gasta 20% de seu salário líquido mensal com a mensalidade de sua casa financiada. Sabendo que seu salário irá receber um aumento de 5% e que a mensalidade de sua casa um reajuste de 12%, qual será o novo percentual do novo salário, gasto com o novo valor da mensalidade da casa própria?
2º) As lojas A e B vendem o mesmo produto por preços diferentes. Se A aumentar seu preço em 8% e B reduzir o seu em 19%, ambas as lojas passarão a vendê-lo por R$ 48,60. Qual é o preço do produto em casa uma das lojas?
3º) Uma loja oferece duas formas de pagamento a seus clientes: 10% de desconto sobre o preço anunciado se o pagamento for à vista, ou o preço anunciado, dividido en duas parcelas iguais: a primeira no ato da compra e a segunda no trigésimo dia após a compra. Determine a taxa de juros efetivamente cobrada pela loja na compra parcelada.
4º) A líquota de um título passou de 8% para 10%. Calcule a taxa de crescimento da líquota (taxa de crescimento da carga tributária).
_______________________________________________________________________________________________________________________________________
1º) Salário: x
Mensalidade da casa: 0,2x
Aumento do salário: 1,05x
Reajuste mensalidade da casa: 1,12•0,2x = 0,224x
0,224x/1,05x = 0,21333333333... ~ 21%
2º) Loja A = x
Loja B = y
1,08x = 48,6 => x = 45 => R$ 45,00
0,81y = 48,6 => y = 60 => R$ 60,00
3º) Essa eu não entendi o enunciado. Maldita dislexia! =\
Mas tentei assim:
Peço anunciado: x
Desconto à vista: 0,9x
Juros efetivo cobrado: y
0,9x ---- 100
' '´ x ---- y
0,9xy = 100x
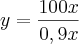
y = 111,111111... ~ 111%
Então os juros efetivamente cobrados seriam 11%, aproximadamente.
4º) Pessoal, essa não sei mesmo nem como calcular... O que eu vou deixa abaixo é TOTALMENTE non-sense, não sei se tá correto
1,08x ---- 100
´1,1x ---- y
1,08xy = 110x
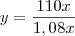
y = 101,851851851851... ~101,85
Logo, a taxa de crescimento da alíquota é de 1,85%







