 por vinicius cruz » Qua Mar 16, 2011 18:06
por vinicius cruz » Qua Mar 16, 2011 18:06
a soma das raizes da equação 4*3^|5x-2|-9^|5x-2|=3 em R vale:
a) 3/5
b) 4/5
c) 6/5
d) 7/5
e) 8/5
nao tenho a resposta certa
-
vinicius cruz
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Dom Mar 06, 2011 12:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por Elcioschin » Qua Mar 16, 2011 20:26
por Elcioschin » Qua Mar 16, 2011 20:26
4*3^|5x-2| - 9^|5x-2|= 3
4*3^|5x-2| - (3²)^|5x-2| = 3
4*3^|5x-2| - (3^|5x-2|)² = 3
(3^|5x-2|)² - 4*3^|5x-2| + 3 = 0 ----> Equação do 2º grau na variável 3^|5x - 2|
Discriminante ----> D = b² - 4ac ----> D = (-4)² - 4*1*3 ----> D = 4 ----> V(D) = 2
Raízes -----> 3^|5x- 2| = (4 + - 2)/2 ---->
3^|5x - 2| = 3¹ ----> |5x - 2| = 1 ----> x = 1/5 ou x = 3/5
3^|5x - 2| = 1 = 3^0 ----> |5x - 2| = 0 ----> x = 2/5
S = 1/5 + 3/5 + 2/5 ----> S = 6/5 ----> Alternativa C
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por MarceloFantini » Qua Mar 16, 2011 20:28
por MarceloFantini » Qua Mar 16, 2011 20:28
Seja
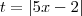
. Então:
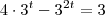
Seja

. Então:
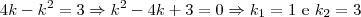
Logo,

ou

. Assim:

ou

. Voltando ao começo:
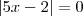
ou
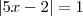
.
Portanto,
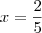
ou
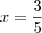
ou
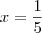
. Somando:
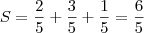
P.S.: Resolvemos juntos Elcio, haha.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por vinicius cruz » Qua Mar 16, 2011 20:36
por vinicius cruz » Qua Mar 16, 2011 20:36
olá fantini
não entendi do t=0 ou t=1 pra baixo
-
vinicius cruz
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Dom Mar 06, 2011 12:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por MarceloFantini » Qua Mar 16, 2011 20:50
por MarceloFantini » Qua Mar 16, 2011 20:50
Olhe o começo do post, o que eu chamei de

. Lembra-se da definição de módulo?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por vinicius cruz » Qua Mar 16, 2011 20:57
por vinicius cruz » Qua Mar 16, 2011 20:57
humm
agora vc me pegou
aeuhuheaueh
ñ lembro da definição de modulo ..vc me ajuda ??
-
vinicius cruz
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Dom Mar 06, 2011 12:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por MarceloFantini » Qua Mar 16, 2011 21:23
por MarceloFantini » Qua Mar 16, 2011 21:23
Se
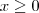
, então

. Se
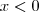
, então
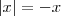
. Aplique isso nas equações e chegará num mesmo resultado. Lembre-se que

pode ser tanto positivo como negativo, por isso você tem que avaliar os dois casos.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Elcioschin » Qui Mar 17, 2011 12:31
por Elcioschin » Qui Mar 17, 2011 12:31
Fantini
Soluções em paralelo.
Se fosse uma corrida de cavalos, eu diria que ganhei por um "nariz" (neste caso nariz = 2 min) ----> ahahah
Elcio
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação exponencial???
por azheng » Sáb Nov 21, 2009 19:47
- 0 Respostas
- 1625 Exibições
- Última mensagem por azheng

Sáb Nov 21, 2009 19:47
Álgebra Elementar
-
- Equação Exponencial
por Adriana Baldussi » Seg Nov 23, 2009 14:41
- 3 Respostas
- 2838 Exibições
- Última mensagem por Molina

Seg Nov 23, 2009 17:07
Álgebra Elementar
-
- Equação Exponencial
por LeonardoSantos » Ter Fev 16, 2010 14:11
- 1 Respostas
- 2828 Exibições
- Última mensagem por Douglasm

Ter Fev 16, 2010 15:46
Funções
-
- Equação exponencial
por cristina » Sex Jun 04, 2010 20:19
- 1 Respostas
- 2241 Exibições
- Última mensagem por Mathmatematica

Sáb Jun 05, 2010 00:27
Sistemas de Equações
-
- Equação exponencial
por nan_henrique » Sáb Jul 10, 2010 13:00
- 1 Respostas
- 2191 Exibições
- Última mensagem por Douglasm

Sáb Jul 10, 2010 13:12
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




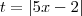 . Então:
. Então: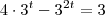
 . Então:
. Então: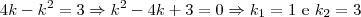
 ou
ou  . Assim:
. Assim: ou
ou  . Voltando ao começo:
. Voltando ao começo: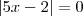 ou
ou 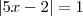 .
.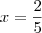 ou
ou 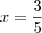 ou
ou 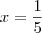 . Somando:
. Somando: 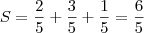



 . Lembra-se da definição de módulo?
. Lembra-se da definição de módulo?


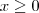 , então
, então  . Se
. Se 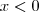 , então
, então 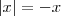 . Aplique isso nas equações e chegará num mesmo resultado. Lembre-se que
. Aplique isso nas equações e chegará num mesmo resultado. Lembre-se que  pode ser tanto positivo como negativo, por isso você tem que avaliar os dois casos.
pode ser tanto positivo como negativo, por isso você tem que avaliar os dois casos.



 .
.
 :
: