Me ajudem a melhorar esta solução a que dei a esta questão, me enviando correções, dicas para enriquecer, etc!!
Quais as seguintes sentenças abertas definem uma relação de equivalência em N (conjunto dos número naturais)?
a) xRy?
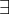 k ? Z tal que x-y=3k
k ? Z tal que x-y=3kb) x divide y;
c) x ? y;
d) m,d,c (x,y)=1;
e) x+y=10.
Solução:
a) i) Para cada x ? N, como x-x=0=3.0, tem-se que : xRx, portanto xRy é reflexiva em N;
ii) Se xRy, então existe k ? Z tal que x-y=3k, consequentemente, y-x= - (x-y)=3(-k); ou seja, yRx, logo xRy é uma relação simétrica em N;
iii) Se xRy e yRz, então
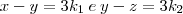 ; para certos inteiros
; para certos inteiros 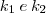 , portanto:
, portanto:x-z=(x-y)+(y-z)=3(
 ) ou seja, xRz, logo xRy é uma relação transitiva;
) ou seja, xRz, logo xRy é uma relação transitiva;logo é equivalente em N;
b) x/y
i) para cada x ? N , como x/x=1 e 1 ? N tem-se que xRx, portanto xRy é reflexiva;
ii) xRy ? x/y não é uma relação de equivalência em N, pois, xRy não é simétrica:
por exemplo: 4/2 ? N, mas 2/4
 a N ;
a N ;c) x ? y; i) xRy ? x ? y não é uma relação de equivalência em N, pois, xRy não é reflexiva e nem simétrica;
d) m.d.c (x,y)=1 ? número primos, portanto, xRy ? m.d.c (x,y)=1 ? Z, mas
 N, logo xRy não é uma relação de equivalência em N;
N, logo xRy não é uma relação de equivalência em N;e) xRy ? x + y = 10
Então R não é uma relação de equivalência em N, pois R não é reflexiva, por
exemplo,
4 + 4 ? 10, ou seja, 4 não está relacionado com 4;
Solução: item a.







