 por WagnerSantos » Sáb Mar 12, 2011 15:16
por WagnerSantos » Sáb Mar 12, 2011 15:16
nao entendi a questão.
Considere a função
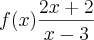
. O conjunto dos valores de x para os quais
![f(x) \in [y\in R : 0< y\leq4] f(x) \in [y\in R : 0< y\leq4]](/latexrender/pictures/4f08c574b5b31618197140adb4166838.png)
é ?
-
WagnerSantos
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Mar 11, 2011 16:21
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: engenharia mecanica
- Andamento: cursando
 por Abelardo » Sáb Mar 12, 2011 15:39
por Abelardo » Sáb Mar 12, 2011 15:39
.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Abelardo » Sáb Mar 12, 2011 17:32
por Abelardo » Sáb Mar 12, 2011 17:32
Tentei resolver, mas fiquei travado no final!
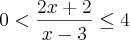
Como tenho duas inequações simultâneas, eu separei e resolvi cada inequação quociente -->
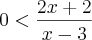
e
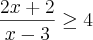
.
Fiz o quadro-resumo de cada uma, mas no final não sei como proceder! Me parece que tenho que fundir os dois quadros.. ai é o meu limite! Espero que te ajude, dê uma luz.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Sáb Mar 12, 2011 19:56
por LuizAquino » Sáb Mar 12, 2011 19:56
Você deve indicar quais são os valores de
x para os quais
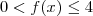
.
Isso significa que você deve resolver a inequação
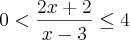
como Abelardo sugeriu.
Se estiver com dificuldades em inequações (ou outros conteúdos do ensino fundamental e médio), por favor veja o tópico:
Aulas de Matemática no YouTubeviewtopic.php?f=120&t=3818
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UFMG) Questão de Função
por Carolziiinhaaah » Sex Ago 13, 2010 17:34
- 1 Respostas
- 8054 Exibições
- Última mensagem por Douglasm

Sex Ago 13, 2010 18:02
Funções
-
- Questão UFMG - função logarítmica
 por kamillanjb » Qua Mar 09, 2011 20:29
por kamillanjb » Qua Mar 09, 2011 20:29
- 5 Respostas
- 19693 Exibições
- Última mensagem por Raissa Dantas

Ter Jul 15, 2014 02:30
Logaritmos
-
- Questão UFMG - função logarítmica
por Raissa Dantas » Ter Jul 15, 2014 02:34
- 0 Respostas
- 1123 Exibições
- Última mensagem por Raissa Dantas

Ter Jul 15, 2014 02:34
Funções
-
- [Função Composta] Questão da UFMG, por favor.
por lucasf10 » Qui Out 02, 2014 17:27
- 1 Respostas
- 2160 Exibições
- Última mensagem por DanielFerreira

Sex Out 03, 2014 01:59
Funções
-
- [POLINÔMIOS] Questão da UFMG envolvendo divisão e função
por Romeo » Qua Nov 16, 2011 16:18
- 0 Respostas
- 1154 Exibições
- Última mensagem por Romeo

Qua Nov 16, 2011 16:18
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
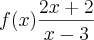 . O conjunto dos valores de x para os quais
. O conjunto dos valores de x para os quais ![f(x) \in [y\in R : 0< y\leq4] f(x) \in [y\in R : 0< y\leq4]](/latexrender/pictures/4f08c574b5b31618197140adb4166838.png) é ?
é ?
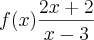 . O conjunto dos valores de x para os quais
. O conjunto dos valores de x para os quais ![f(x) \in [y\in R : 0< y\leq4] f(x) \in [y\in R : 0< y\leq4]](/latexrender/pictures/4f08c574b5b31618197140adb4166838.png) é ?
é ?

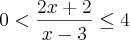 Como tenho duas inequações simultâneas, eu separei e resolvi cada inequação quociente -->
Como tenho duas inequações simultâneas, eu separei e resolvi cada inequação quociente --> 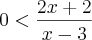 e
e 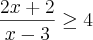 .
.
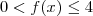 .
.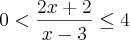 como Abelardo sugeriu.
como Abelardo sugeriu.