Questão prova concurso (Elipse)

[fernandocez]

Caros amigos espero que todos aproveitaram bem o feriado e eu continuo estudando para o concurso do Estado (RJ). Eu acho que não vai dar tempo de eu aprender tudo é muita matéria. Essa questão é sobre elipse, eu já estudei na faculdade mas não lembro de mais nada, procurei num livro e consegui uma fórmula mas me perdi nos cálculos. Se tiver uma forma mais simples vai ajudar. Vamos a questão.

58. O ponto P pertence à curva de equação =1, cujos focos são F e F'. A maior área possível do triângulo PFF' é:
Resp: 18

Encontrei com ajuda do livro (não sei se tá certo):
a =
b = 3
a²+b²+c² = 45=9+c²
c²=6

Encontrei uma fórmula:
PF1+PF2=2a

Substituí na fórmula do livro:

Comecei a substituir mas me perdi nos cálculos. Existe uma maneira mais fácil? Aguardo e obrigado.

[Elcioschin]

fernandocez

Quase tudo que você fez está correto. O único erro foi c² = 36 ----> c = 6

Faltou você calcular a base do triângulo ----> F1F2 = 2c = 12

A altura do triângulo PF1F2 é a ordenada yP do ponto P(xP, yP).

Sem esta informação é impossível calcular a área.

Acontece que ele pediu a MAIOR área possível!!!!

Note então o seguinte:

1) Imagine que o ponto P coincide com o vértice esquerdo do eixo maior 2a. Neste caso yP = 0 e a área é nula.
2) Imagine agora o ponto P se deslocando ao longo da elipse, para a direita.
3) Quando o ponto P coincidir com o vértice direito do eixo maior 2a ----> yP = 0 e a área também é nula.
4) No meio do caminho, portanto vai existir um ponto P para o qual a área é máxima.
5) Este ponto é exatamente o vértice superior do eixo menor 2b ----> yP = b = 3

Smáx = F1F2*b/2 ---> Smáx = 12*3/2 ----> Smáx = 18

[LuizAquino]

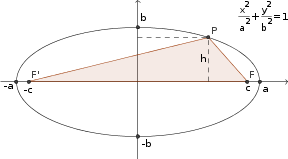
Eu vou apenas ilustrar o que o colega Elcioschin respondeu.

Considere o gráfico abaixo.

elipse.png (5.45 KiB) Exibido 1792 vezes

Como a base do triângulo F'PF é sempre a mesma (e mede 2c), esse triângulo terá a maior área quando ele tiver a maior altura.

Note que essa maior altura ocorre quando h=b.