Seja A = {1,2,3}. Considere as seguintes relações em A:
 = {(1,2);(1,1);(2,2);(2,1);(3,3)}
= {(1,2);(1,1);(2,2);(2,1);(3,3)}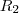 = {(1,1);(2,2);(3,3);(1,2);(2,3)}
= {(1,1);(2,2);(3,3);(1,2);(2,3)} = {(1,1);(2,2);(1,2);(2,3);(3,1)}
= {(1,1);(2,2);(1,2);(2,3);(3,1)}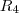 = AxA;
= AxA; =
= 
Quais são reflexivas?Simétrica? anti-simétricas? e Transitivas?
Solução:
Reflexivas:
 ;
;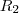 ;
;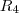 ;
;Pergunto: Porque o conjunto vazio não é reflexivo?
Simétricas:
 ;
;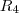 ;
;Pergunto: o Conjunto Vazio é simétrico ou não?Porquê?
Transitivas:
 é transitiva pois, (1,2)
é transitiva pois, (1,2)
 ;(2,2)
;(2,2)
 e obviamente implica que (1,2)
e obviamente implica que (1,2)
 ; como também (2,1)
; como também (2,1)
 ;(1,2)
;(1,2)
 implica que (2,2)
implica que (2,2)
 ; ok?
; ok?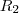 não é transitiva pois, (1,2)
não é transitiva pois, (1,2)
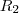 ;(2,3)
;(2,3)
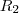 , mas (1,3)
, mas (1,3)
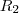 ;
; não é transitiva pois (1,2)
não é transitiva pois (1,2)
 ; (2,3)
; (2,3)
 ; mas, (3,1)
; mas, (3,1)
 ;
;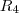 é transitiva;
é transitiva;Pergunto: conjunto Vazio é transitivo, porquê? ;
Anti-Simétrica:
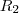 ;
;  ;
;  .
.

 não é reflexiva porque, obviamente, não contém os elementos do tipo (a, a), para todo a em A.
não é reflexiva porque, obviamente, não contém os elementos do tipo (a, a), para todo a em A. .
. ;
;  ; mas,
; mas,  ;
; "
"
 não é reflexiva? Porque (3, 3) não está em
não é reflexiva? Porque (3, 3) não está em  . Novamente, note que esse problema não ocorre em
. Novamente, note que esse problema não ocorre em  Luiz;
Luiz;

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.