R1 = {(1,1), (1,2)}, R4 = {(1,1), (2,2), (3,3)},
R2 = {(1,1), (2,3), (4,1)}, R5 = W x W
R3 = {(1,3), (2,4)}
Diga se cada uma das relações é ou não: (1) simétrica, (2) anti-simétrica, (3) transitiva, (4) reflexiva.
(1) Em R1, (1,2) ? R1, mas (2,1)
 a R1, não é simétrica;
a R1, não é simétrica;Em R2, (2,3) ? R2, mas (3,2)
 a R2, não é simétrica, mesmo para (4,1);
a R2, não é simétrica, mesmo para (4,1);Em R3, (1,3) ? R3, mas (3,1)
 a R3, não é simétrica, mesmo para (2,4);
a R3, não é simétrica, mesmo para (2,4);Em R4, (1,1) ? R4, não necessariamente elementos distintos, é simétrica a relação;
Em R5, há todas as possibilidades de relações possíveis e também simétrica.
(2) Segundo o autor da questão apenas R5 não é anti-simétrica, mas se o conjunto é simétrico isso não é pré-requisito para ser anti-simétrico?Porque não?
(3) O autor da questão afirma ser todas transitivas, por quê? Exemplo em R2, se (1,1) ? R2 e (4,1) ? R2 mas (1,4)
 a R2. E porque R3 seria transitiva?
a R2. E porque R3 seria transitiva?(4) Somente R5 é reflexiva, pois a definição deixa claro que cada elemento de W deve ser considerado.


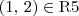
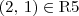
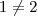 .
.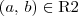 e
e 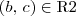 , temos que
, temos que 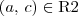 . Por exemplo,
. Por exemplo, 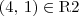 ,
, 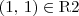 e obviamente
e obviamente 
