 por heroncius » Ter Set 18, 2007 21:50
por heroncius » Ter Set 18, 2007 21:50
uma empresa de transporte estabelece por viagem o preço individual da passagem (p) em função da quantidade (q) de passageiros através da relação p= -0,2 q + 100. com 0<q<500.nestas condições para q a quantia arrecadada pela empresa, em cada viagem, seja máxima, o preço da passagem deve ser , em reais de:
a)45 b)35 c)40 d)50 e)55
desde já agradeço a atenção!!!
Paulo Herôncio
-
heroncius
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Ter Jul 31, 2007 11:22
 por admin » Qua Set 19, 2007 14:46
por admin » Qua Set 19, 2007 14:46
heroncius escreveu:uma empresa de transporte estabelece por viagem o preço individual da passagem (p) em função da quantidade (q) de passageiros através da relação p= -0,2 q + 100. com 0<q<500.nestas condições para q a quantia arrecadada pela empresa, em cada viagem, seja máxima, o preço da passagem deve ser , em reais de:
a)45 b)35 c)40 d)50 e)55
desde já agradeço a atenção!!!
Paulo Herôncio
Olá Paulo.
Este é um problema de otimização.
Primeiro temos que destacar que a
quantia arrecadada em cada viagem é o produto

, ou seja, o preço de cada passagem multiplicado pelo número de passageiros.

: quantia arrecadada em cada viagem
Note que este é o valor que queremos maximizar em nossa otimização.
Como:
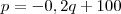
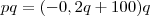
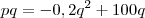
Vamos chamar esta função da arrecadação de

.
Como é uma função em

, temos:
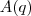
: função arrecadação
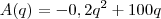
Veja que
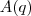
é uma função do segundo grau, formando uma parábola côncava para baixo porque o coeficiente de
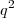
é negativo.
Esta informação garante que
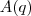
possui um máximo.
Você já deve ter visto que o valor máximo de uma função do 2º grau:
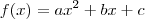
É dado por:
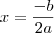
De qualquer forma, tendo ou não visto, veja como é simples chegarmos à esta conclusão:
As raízes da função de 2º grau são:
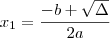
e
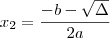
(considerando

)
O valor máximo de

será dado quando
x for a média aritmética entre as raízes

e
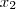
(olhe um gráfico de parábola).
![Max[f(x)] \Leftrightarrow x = \frac{x_1 + x_2}{2} Max[f(x)] \Leftrightarrow x = \frac{x_1 + x_2}{2}](/latexrender/pictures/ba23e040084db4c80753dbbae029362a.png)
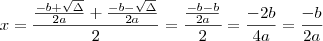
(repare que caso a parábola seja côncava para cima, a função possuirá valor
mínimo e o cálculo será análogo)
Voltando para a função arrecadação:
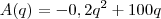
Então, seu valor máximo será quando:
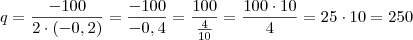
(passageiros)
E por fim, respondendo à questão, precisamos saber qual o preço da passagem para esta quantidade de passageiros:
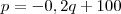
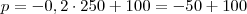

Reais
(alternativa d)Paulo, dois comentários:
1) repare que o intervalo citado no enunciado
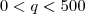
é justamente o intervalo entre as raízes da função arrecadação.
Esta condição da quantidade passageiros garante que a arrecadação fique sempre positiva!
2) Uma outra pergunta que poderia ser feita e facilmente respondida após esta resolução é a seguinte:
Qual então será a arrecadação máxima obtida pela empresa em cada viagem?
Como sabemos que:
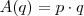
Então:
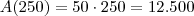
(Reais)
Espero ter ajudado.
Abraço!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por heroncius » Qua Set 19, 2007 21:59
por heroncius » Qua Set 19, 2007 21:59
olá Fábio...ajudou muito.
mais uma vez obrigado
abraço!!!
-
heroncius
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Ter Jul 31, 2007 11:22
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- questão da ESA-2006
por heroncius » Dom Set 09, 2007 16:37
- 3 Respostas
- 6541 Exibições
- Última mensagem por admin

Dom Set 09, 2007 22:11
Álgebra Elementar
-
- II questão da ESA-2006
por heroncius » Qua Set 12, 2007 13:51
- 3 Respostas
- 4330 Exibições
- Última mensagem por admin

Qui Set 13, 2007 14:51
Álgebra Elementar
-
- UNIFEI 2006- Probabilidade
por Luiz C » Qua Jan 13, 2010 23:50
- 2 Respostas
- 3224 Exibições
- Última mensagem por Luiz C

Qui Jan 14, 2010 17:35
Estatística
-
- COMBINATORIA TRANSPETRO 2006
por fefehawaii » Ter Mai 03, 2011 22:23
- 1 Respostas
- 1716 Exibições
- Última mensagem por FilipeCaceres

Ter Mai 03, 2011 23:52
Estatística
-
- prova da uesb 2006.1
por Matheusvc1 » Dom Dez 08, 2013 15:30
- 1 Respostas
- 5083 Exibições
- Última mensagem por DanielFerreira

Ter Fev 11, 2014 16:17
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , ou seja, o preço de cada passagem multiplicado pelo número de passageiros.
, ou seja, o preço de cada passagem multiplicado pelo número de passageiros.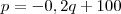
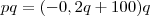
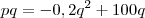
 .
. , temos:
, temos: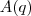 : função arrecadação
: função arrecadação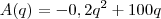
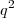 é negativo.
é negativo.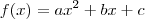
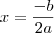
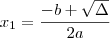 e
e 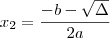
 )
) será dado quando
será dado quando  e
e 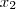 (olhe um gráfico de parábola).
(olhe um gráfico de parábola).![Max[f(x)] \Leftrightarrow x = \frac{x_1 + x_2}{2} Max[f(x)] \Leftrightarrow x = \frac{x_1 + x_2}{2}](/latexrender/pictures/ba23e040084db4c80753dbbae029362a.png)
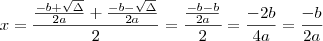
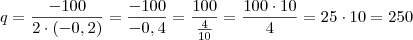 (passageiros)
(passageiros)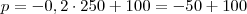
 Reais
Reais 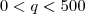 é justamente o intervalo entre as raízes da função arrecadação.
é justamente o intervalo entre as raízes da função arrecadação.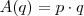
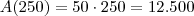 (Reais)
(Reais)


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.