 por fernandocez » Ter Mar 01, 2011 12:11
por fernandocez » Ter Mar 01, 2011 12:11
Caro amigos, venho mais uma vez pedir ajuda. A questão envolvendo sistema de equações tá me dando dor de cabeça. Vamos a bendita questão.
54. Em certa papelaria todos os lápis tem o mesmo preço, todas as borrachas tem o mesmo preço e todas as canetas tem o mesmo preço. Comprando 8 lápis, 4 borrachas e 3 canetas você pagará R$ 21,60. Comprando 6 lápis, 8 borrachas e 4 canetas você pagará R$ 27,20. Uma compra de 20 lápis, 20 borrachas e 11 canetas custará:
resposta: R$ 76,00.
Eu fiz o seguinte:
8l + 4b+ 3c = 21,60
6l + 8b + 4c = 27,20
20l + 20b + 11c = x
Eu ía tentar por escalonamento de sistema, multiplicar umas das esquações e somar com outra prá cancelar uma das incógnitas. Mas percebi que tinha o "x", achei que assim não ía dar. Resolvi fazer por adição só nas 2 primeiras mas não deu certo. Só com as duas primeiras no sist. de escalonamento o "c" volta a aparecer:
8l + 4b+ 4c = 21,60
14l +- 8b = 4,8
Se eu continuasse o "c" voltaria e tinha que fazer de novo.
Tem um modo mais fácil de encontrar os valores de L, B, C? Na prova depende de tempo e é o que não tem. Aguardo uma ajuda.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Ter Mar 01, 2011 12:41
por LuizAquino » Ter Mar 01, 2011 12:41
Dica: multiplique toda a segunda equação por 2 e em seguida some com a primeira equação.
Editado pela última vez por
LuizAquino em Ter Mar 01, 2011 12:42, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Renato_RJ » Ter Mar 01, 2011 12:42
por Renato_RJ » Ter Mar 01, 2011 12:42
Bom dia Fernando, tudo em paz ??
Seguinte amigão, eu consegui resolver usando escalonamento mesmo, veja:
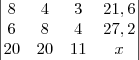
Eu fiz
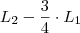
para eliminar o 6 da primeira coluna da segunda linha, veja:
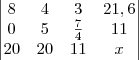
Depois eu fiz
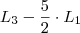
para eliminar o 20 da primeira coluna da terceira linha, veja:
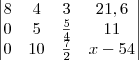
Para eliminar o 10 (da segunda coluna da terceira linha) eu simplesmente fiz
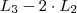
, então:
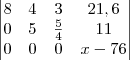
Logo, teremos:
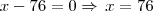
Espero ter ajudado..
[ ] 's
Renato
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por fernandocez » Ter Mar 01, 2011 13:01
por fernandocez » Ter Mar 01, 2011 13:01
LuizAquino escreveu:Dica: multiplique toda a segunda equação por 2 e em seguida some com a primeira equação.
Renato_RJ escreveu:Bom dia Fernando, tudo em paz ??
Seguinte amigão, eu consegui resolver usando escalonamento mesmo, veja:
Obrigado pessoal, vcs são muito feras, seu estivesse nesse nível passaria com folga no concurso, mas tenho que estudar muito mesmo. Um abração.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por Renato_RJ » Ter Mar 01, 2011 13:06
por Renato_RJ » Ter Mar 01, 2011 13:06
Fernando, se puder compre os livros da SBM (Sociedade Brasileira de Matemática) da coleção Professor de Matemática, são os livros adotados nos dois primeiros períodos do curso de licenciatura da UNIRIO, são excelentes pois cobrem toda a matemática do fundamental até o médio mas com uma profundidade mais apropriada ao professor, explicando conceitos e terminologias...
Se você se cadastra na SBM recebe um desconto de 25% para cada compra, a maioria desses livros acaba custando R$ 18,00, acho que vale a pena (eles entregam pelos correios)...
Segue o link para a coleção da qual eu falei:
http://loja.sbm.org.br/index.php?cPath= ... 09b81659ae[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por LuizAquino » Ter Mar 01, 2011 13:41
por LuizAquino » Ter Mar 01, 2011 13:41
Olá fernandocez,
Uma curiosidade: onde você fez a sua graduação em Licenciatura em Matemática?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fernandocez » Ter Mar 01, 2011 20:56
por fernandocez » Ter Mar 01, 2011 20:56
Renato_RJ escreveu:Fernando, se puder compre os livros da SBM (Sociedade Brasileira de Matemática) da coleção Professor de Matemática, são os livros adotados nos dois primeiros períodos do curso de licenciatura da UNIRIO, são excelentes pois cobrem toda a matemática do fundamental até o médio mas com uma profundidade mais apropriada ao professor, explicando conceitos e terminologias...
Valeu a dica renato vou comprar sim, uma pergunta: a linguagem não é muito "pesada" desses livros? Porque eu tenho alguns da coleção Fundamentos de mat. elementar e acho muito difícil entender.
LuizAquino escreveu:Olá fernandocez,
Uma curiosidade: onde você fez a sua graduação em Licenciatura em Matemática?
O Luiz, vc sempre me ajudando nas questões. Sobre o meu curso, eu fiz na Unigranrio em Caxias - RJ, mas não culpem a instituição eu é que caí de paraquedas lá. Eu comecei a fazer informática (2 períodos), desisti e troquei pela Matemática pra arrumar emprego com mais facilidade o que não aconteceu. Eu me formei em 2009 e até agora não consegui nenhum colégio prá lecionar. Já coloquei uns 40 currículos mas nenhum vingou, nem se quer fui a uma entrevista. Agora tô apostando nesse concurso e nos próximos.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por Renato_RJ » Ter Mar 01, 2011 21:48
por Renato_RJ » Ter Mar 01, 2011 21:48
fernandocez escreveu:Renato_RJ escreveu:Fernando, se puder compre os livros da SBM (Sociedade Brasileira de Matemática) da coleção Professor de Matemática, são os livros adotados nos dois primeiros períodos do curso de licenciatura da UNIRIO, são excelentes pois cobrem toda a matemática do fundamental até o médio mas com uma profundidade mais apropriada ao professor, explicando conceitos e terminologias...
Valeu a dica renato vou comprar sim, uma pergunta: a linguagem não é muito "pesada" desses livros? Porque eu tenho alguns da coleção Fundamentos de mat. elementar e acho muito difícil entender.
Grande Fernando, essa coleção é do Iezzi certo ?? Se for, é a mesma que eu tenho aqui, e te digo, os livros da SBM são mais profundos pois trazem as demonstrações necessárias para a compreensão do conteúdo, fora que seus exercícios são bem mais complicados. Mas se você tem o Iezzi, estude por ele, é um excelente livro...
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Sistema equações] questão de concurso 2011
por fernandocez » Qua Out 05, 2011 22:32
- 9 Respostas
- 6441 Exibições
- Última mensagem por fernandocez

Sáb Out 08, 2011 15:33
Sistemas de Equações
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4502 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- SISTEMA DE EQUAÇÃO PROVA SENAI
por hatredshadows » Sex Nov 08, 2013 08:17
- 3 Respostas
- 3312 Exibições
- Última mensagem por e8group

Sex Nov 08, 2013 20:53
Sistemas de Equações
-
- Sistema de equações
por Cleyson007 » Sex Set 12, 2008 12:47
- 6 Respostas
- 5555 Exibições
- Última mensagem por Cleyson007

Qua Jun 03, 2009 17:25
Sistemas de Equações
-
- Sistema de Equações
por Cleyson007 » Qua Mai 27, 2009 14:01
- 3 Respostas
- 3352 Exibições
- Última mensagem por Cleyson007

Qui Mai 28, 2009 17:51
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



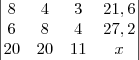
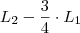 para eliminar o 6 da primeira coluna da segunda linha, veja:
para eliminar o 6 da primeira coluna da segunda linha, veja: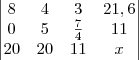
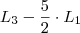 para eliminar o 20 da primeira coluna da terceira linha, veja:
para eliminar o 20 da primeira coluna da terceira linha, veja: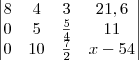
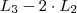 , então:
, então: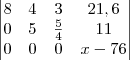
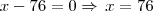
 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: