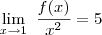
(a)
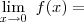
(b)
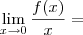
Sinceramente , não sei muito o que tentar.Só consegui chegar a conclusão que
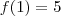 , e depois tentei achar algumas funcoes para criar desigualdades validas para x proximo de 0 e poder aplicar o teorema do confronto , mas nada de sucesso, já que nao creio que posso afirmar algo sobre
, e depois tentei achar algumas funcoes para criar desigualdades validas para x proximo de 0 e poder aplicar o teorema do confronto , mas nada de sucesso, já que nao creio que posso afirmar algo sobre  para x proximo de 0.
para x proximo de 0.Agradeço já por qualquer esclarecimento!


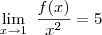 . Para cada uma delas, teríamos uma resposta diferente para os outros limites desejados.
. Para cada uma delas, teríamos uma resposta diferente para os outros limites desejados.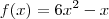 . Nós teríamos:
. Nós teríamos: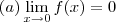
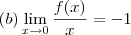
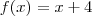 . Nós teríamos:
. Nós teríamos: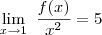
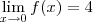
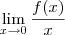 não existe, pois os seus limites laterais são distintos:
não existe, pois os seus limites laterais são distintos: 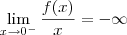 e
e 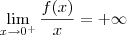 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.