Observe a figura 1 que representa um leitor de áudio na posição de início de leitura.Os suportes
circulares A e B têm 1 cm de raio e uma fita de 90 m está totalmente enrolada em A formando uma
coroa circular de espessura 1,5 cm. A leitura da fita é feita pela peça C a uma velocidade constante.
À medida que a fita passa, nos suportes A e B, formam-se duas coroas circulares com raios maiores x
e y, respectivamente, como sugere a figura abaixo.
A . Esboce o gráfico que mostra o comprimento da fita enrolada em A, em função do tempo de leitura.
B. Calcule y em função de x.
(detalhe...eu n consigo ver os dados nessa questão, para mim esta faltando algo! Me ajudem, por favor!)
Resposta: b)
![\sqrt[2]{7,5-x²}, 1<=x<=2.5](/latexrender/pictures/d90249107c86fc7647cb3097ad123280.png "\sqrt[2]{7,5-x²}, 1<=x<=2.5")
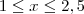teremos a equação: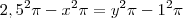
.
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)