 por Regina » Sáb Fev 26, 2011 16:21
por Regina » Sáb Fev 26, 2011 16:21
Estou a meio de um exercício e surgiu-me outra dúvida.
Cheguei a esta equação e tenho que saber o valor de t, mas como faço?
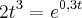
-
Regina
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sex Fev 25, 2011 14:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: curso técnico em química
- Andamento: cursando
 por LuizAquino » Sáb Fev 26, 2011 16:47
por LuizAquino » Sáb Fev 26, 2011 16:47
Regina escreveu: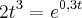
Por favor, coloque o texto completo do exercício.
Não há uma forma analítica de resolver essa equação. Ela só pode ser resolvida usando alguma estratégia numérica.
Note que se você efetuar o logaritmo neperiano (ou natural) em ambos os membros, teria algo como:

Aplicando as propriedades de logaritmo, a equação fica:

A partir daqui não há o que fazer analiticamente! Só mesmo usando alguma estratégia numérica!
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Regina » Sáb Fev 26, 2011 17:15
por Regina » Sáb Fev 26, 2011 17:15
Então é assim. Eu tenho duas equações que indicam a concentração de um medicamento com o passar do tempo. os medicamentos são administrados a duas pessoas diferentes no mesmo instante, t=0, e o enunciado pergunta quando é que as concentrações dos medicamentos nas duas pessoas voltam a ser iguais.
As duas equações são: Indivúduo A

e para o Indivíduo C

Eu igualei as equações

e fui tentando simplificar até me dar

Só se a resolução não for para igualar as expressões...
-
Regina
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sex Fev 25, 2011 14:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: curso técnico em química
- Andamento: cursando
 por LuizAquino » Sáb Fev 26, 2011 17:24
por LuizAquino » Sáb Fev 26, 2011 17:24
Regina escreveu:As duas equações são: Indivúduo A

e para o Indivíduo C

Eu igualei as equações

e fui tentando simplificar até me dar

A sua simplificação está errada! O correto nesse caso seria você dividir toda a equação por
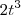
, ficando com:

Em seguida, você deve efetuar o logaritmo neperiano em ambos os membros:

Aplicando as propriedades de logaritmo, teremos:

Tente continuar a partir daqui.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação exponencial???
por azheng » Sáb Nov 21, 2009 19:47
- 0 Respostas
- 1624 Exibições
- Última mensagem por azheng

Sáb Nov 21, 2009 19:47
Álgebra Elementar
-
- Equação Exponencial
por Adriana Baldussi » Seg Nov 23, 2009 14:41
- 3 Respostas
- 2836 Exibições
- Última mensagem por Molina

Seg Nov 23, 2009 17:07
Álgebra Elementar
-
- Equação Exponencial
por LeonardoSantos » Ter Fev 16, 2010 14:11
- 1 Respostas
- 2826 Exibições
- Última mensagem por Douglasm

Ter Fev 16, 2010 15:46
Funções
-
- Equação exponencial
por cristina » Sex Jun 04, 2010 20:19
- 1 Respostas
- 2239 Exibições
- Última mensagem por Mathmatematica

Sáb Jun 05, 2010 00:27
Sistemas de Equações
-
- Equação exponencial
por nan_henrique » Sáb Jul 10, 2010 13:00
- 1 Respostas
- 2190 Exibições
- Última mensagem por Douglasm

Sáb Jul 10, 2010 13:12
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
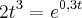

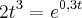




 e para o Indivíduo C
e para o Indivíduo C 



e para o Indivíduo C
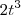 , ficando com:
, ficando com:




 .
.



