 por Higor » Seg Fev 21, 2011 15:52
por Higor » Seg Fev 21, 2011 15:52
Boa Tarde Pessoal.
Estou fazendo um exercicio, mas esta dando um valor nao muito convencional, vamos la
talvez vcs possam me ajudar:
EXERCICIO:
![\frac{dy}{dt} = \frac{t.e^t}{y.\sqrt[]{1+y^2}} \frac{dy}{dt} = \frac{t.e^t}{y.\sqrt[]{1+y^2}}](/latexrender/pictures/5f847e3936c3f481fac649db4683baaf.png)
Começei da seguinte forma:

y
![\sqrt[]{1+y^2} dy = [tex]\int_{}^{} \sqrt[]{1+y^2} dy = [tex]\int_{}^{}](/latexrender/pictures/dae387b81034da8e0bbcc43c20986d9d.png)
t.e^t dt
na parte t.e^t dt
resolvi por partes
u= t dv= e^t
du = 1 v= e^t
u.v -
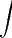
v. du
=
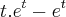
=

y
![\sqrt[]{1+y^2} dy = t. e^t - e^t \sqrt[]{1+y^2} dy = t. e^t - e^t](/latexrender/pictures/3b4ada5480c46a22ffa4be9fb54535db.png)
bom, agora a primeira parte

y
![\sqrt[]{1+y^2} dy \sqrt[]{1+y^2} dy](/latexrender/pictures/2f494de82d546a2b6a6e981315792068.png)
u=1+y^2
du= 2y dy
du/2= y dy
assim :
![\frac{1}{2} \int_{}^{}\sqrt[]{u} du \frac{1}{2} \int_{}^{}\sqrt[]{u} du](/latexrender/pictures/3f1a6bc8c1e101b62123d6f16d50a43d.png)
subistitui
raiz de u por u^1/2
e integrei
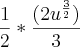
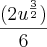
voltando o valor de u
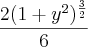
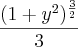
ai chego até esse ponto:
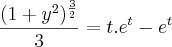
nao sei se esta certo, por favor me ajudem ai.
-
Higor
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Fev 20, 2011 17:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por Marcampucio » Seg Fev 21, 2011 16:48
por Marcampucio » Seg Fev 21, 2011 16:48
Está tudo certo, sim.
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por Higor » Seg Fev 21, 2011 17:04
por Higor » Seg Fev 21, 2011 17:04
Mas, ainda nao chegou ao fim ?? tem mais alguma coisa não tem ???
-
Higor
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Fev 20, 2011 17:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Outra - fração
por cidaiesbik » Qui Mai 21, 2009 10:35
- 3 Respostas
- 3572 Exibições
- Última mensagem por cidaiesbik

Seg Mai 25, 2009 10:17
Desafios Enviados
-
- Outra Dúvida
por rodsales » Sáb Jun 06, 2009 21:41
- 1 Respostas
- 1501 Exibições
- Última mensagem por Marcampucio

Sáb Jun 06, 2009 22:38
Trigonometria
-
- Outra dúvida
por rodsales » Qui Jun 18, 2009 22:12
- 1 Respostas
- 1443 Exibições
- Última mensagem por Marcampucio

Sex Jun 19, 2009 00:48
Trigonometria
-
- Outra dúvida.
por rodsales » Seg Out 12, 2009 09:56
- 1 Respostas
- 1520 Exibições
- Última mensagem por Marcampucio

Seg Out 12, 2009 11:59
Trigonometria
-
- Outra questão
por GABRIELA » Ter Out 20, 2009 16:37
- 1 Respostas
- 1452 Exibições
- Última mensagem por carlos r m oliveira

Qua Out 21, 2009 08:48
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{dy}{dt} = \frac{t.e^t}{y.\sqrt[]{1+y^2}} \frac{dy}{dt} = \frac{t.e^t}{y.\sqrt[]{1+y^2}}](/latexrender/pictures/5f847e3936c3f481fac649db4683baaf.png)
 y
y ![\sqrt[]{1+y^2} dy = [tex]\int_{}^{} \sqrt[]{1+y^2} dy = [tex]\int_{}^{}](/latexrender/pictures/dae387b81034da8e0bbcc43c20986d9d.png) t.e^t dt
t.e^t dt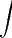 v. du
v. du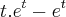
 y
y ![\sqrt[]{1+y^2} dy = t. e^t - e^t \sqrt[]{1+y^2} dy = t. e^t - e^t](/latexrender/pictures/3b4ada5480c46a22ffa4be9fb54535db.png)
 y
y ![\sqrt[]{1+y^2} dy \sqrt[]{1+y^2} dy](/latexrender/pictures/2f494de82d546a2b6a6e981315792068.png)
![\frac{1}{2} \int_{}^{}\sqrt[]{u} du \frac{1}{2} \int_{}^{}\sqrt[]{u} du](/latexrender/pictures/3f1a6bc8c1e101b62123d6f16d50a43d.png)
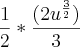
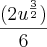
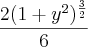
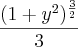
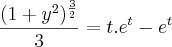





 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.