 por Renato_RJ » Dom Fev 20, 2011 19:05
por Renato_RJ » Dom Fev 20, 2011 19:05
Boa tarde amigos !!!
Hoje me deparei com uma questão de aritmética modular e não sei se a demonstração está errada, poderiam verificar por favor ? A questão é:
Prove que:
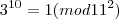
Eu fiz assim:
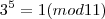
Me valendo da propriedade básica da aritmética modular, fiz o seguinte:
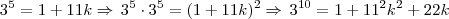
É aqui que não sei se está certo, pois quando desenvolvo o binômio chego no
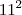
mas aparece o 22k que acaba "atrapalhando" quando quero voltar para a definição de módulo... Alguém tem alguma ideia ou sugestão de método para a demonstração ?
Grato a todos,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Renato_RJ » Dom Fev 20, 2011 21:29
por Renato_RJ » Dom Fev 20, 2011 21:29
Luiz, Fantini, Molina, alguém ???
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Molina » Seg Fev 21, 2011 01:04
por Molina » Seg Fev 21, 2011 01:04
Boa noite, Renato.
Faz um bom tempo que não mexo com este assunto e confesso que não lembro da maior parte das propriedades.
Mas o 22k que "sobrou" não tem nenhuma relação com
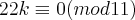
Se não tiver nada a ver peço desculpas mas se for o caso vou revisar o conteúdo.
Abraços.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Renato_RJ » Seg Fev 21, 2011 10:47
por Renato_RJ » Seg Fev 21, 2011 10:47
Molina, muito obrigado pela atenção... Mas estou nesta mesma dúvida, se o que você escreveu estiver certo, aí a demonstração "sai fácil", como hoje irei a universidade para ajustar os detalhes do projeto que iniciarei este período, aproveito para pegar alguma dica com a professora de álgebra, aí posto a demonstração completa aqui..
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Renato_RJ » Ter Fev 22, 2011 09:40
por Renato_RJ » Ter Fev 22, 2011 09:40
Molina, não consegui falar com a professora de álgebra, mas parece que resolvi o problema, veja:
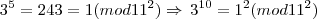
Simples e rápido, e eu aqui "batendo cabeça"... rss...
Valeu pela ajuda

Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Molina » Ter Fev 22, 2011 10:54
por Molina » Ter Fev 22, 2011 10:54
As vezes procuramos dificuldades onde não tem, hahah!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Aritmética modular
por Lorenzo » Qui Jun 17, 2010 22:41
- 1 Respostas
- 1663 Exibições
- Última mensagem por Tom

Sex Jul 02, 2010 23:28
Sistemas de Equações
-
- Aritmética- Duvida em questão do livro praticando aritmética
por wellkirby » Sex Ago 28, 2015 17:37
- 1 Respostas
- 3500 Exibições
- Última mensagem por wellkirby

Seg Set 07, 2015 23:15
Aritmética
-
- [inequação modular] DÚVIDA SIMPLES EM INEQUAÇÃO MODULAR
por brunocunha2008 » Sex Set 13, 2013 22:37
- 1 Respostas
- 7401 Exibições
- Última mensagem por Rafael Henrique

Qui Jan 03, 2019 14:39
Inequações
-
- [Aritmética] Progressão Aritmética.
por Pessoa Estranha » Qua Ago 28, 2013 22:11
- 2 Respostas
- 5637 Exibições
- Última mensagem por Pessoa Estranha

Qui Ago 29, 2013 16:06
Aritmética
-
- Funçao modular
por Fiel8 » Sex Jul 10, 2009 19:25
- 1 Respostas
- 2622 Exibições
- Última mensagem por Molina

Sex Jul 10, 2009 21:50
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
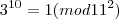
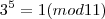
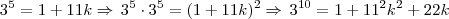
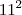 mas aparece o 22k que acaba "atrapalhando" quando quero voltar para a definição de módulo... Alguém tem alguma ideia ou sugestão de método para a demonstração ?
mas aparece o 22k que acaba "atrapalhando" quando quero voltar para a definição de módulo... Alguém tem alguma ideia ou sugestão de método para a demonstração ?

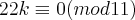

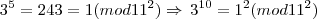



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.