 por john » Seg Fev 14, 2011 16:13
por john » Seg Fev 14, 2011 16:13
g(x)= (2+x)*e^x
Mostre que g'(x)=(3+x)e^x
Comecei a fazer pela regra do produto.
g'(x)= (2+x)' * e^x + (2+x) * (e^x)'
g'(x)= 1*e^x + (2+x) * 1* (e^x)
g'(x)= e^x + (2+x) * (e^x)
Mas não consigo provar o que é pedido.
Alguém ajuda? Obrigado.
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Seg Fev 14, 2011 22:58
por LuizAquino » Seg Fev 14, 2011 22:58
john escreveu:Mas não consigo provar o que é pedido.
Você praticamente já terminou a questão!
Você parou em:
g'(x)= e^x + (2+x) * (e^x)
Mas, isso é o mesmo que:
g'(x)= e^x + 2e^x + xe^x
De onde temos que:
g'(x)= 3e^x + xe^x
Mas, isso é o mesmo que:
g'(x)= (3+x)e^x
ObservaçãoParece que você não está muito afiado com os conteúdos mais fundamentais de Matemática. Para fazer uma revisão desses conteúdos, indico para você o Canal do Nerckie no YouTube:
http://www.youtube.com/nerckie
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por john » Ter Fev 15, 2011 12:41
por john » Ter Fev 15, 2011 12:41
Sim, luiz tem razão. Não estou muito afiado com os conteúdos fundamentais de Matemática. Obrigado pela recomendação.
Estava treinando outro exercício do género.
Provar que f(x)= ln
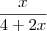
= f'(x)=
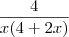
Fiz a derivada pela regra da divisão e obtive:
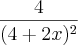
Agora seguindo a derivada do logaritmo fiquei com
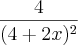
/
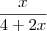
E depois também diz:
Prove que f''(x)=
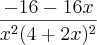
Fazendo a derivada fiquei com:
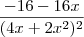
Sei que tenho so exercícios praticamente certos. Só não sei fazer a simplificação final.
Obrigado pela atenção!
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Ter Fev 15, 2011 14:51
por LuizAquino » Ter Fev 15, 2011 14:51
Exercício:
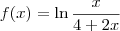
, calcule f'.
Usando regra da cadeia:
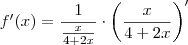
Usando a regra do quociente:
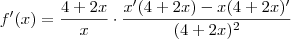
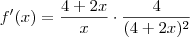
Simplificando os termos (4+2x) e (4+2x)²:
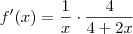
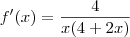
john escreveu:Sim, luiz tem razão. Não estou muito afiado com os conteúdos fundamentais de Matemática. Obrigado pela recomendação.
Tenha certeza que se você investir um tempo para assistir aos vídeos e revisar o conteúdo provavelmente não vai mais errar esse tipo de questão.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por john » Ter Fev 15, 2011 15:01
por john » Ter Fev 15, 2011 15:01
Obrigado Luiz. Nem sequer conhecia essa regra da cadeia. Vou pesquisar sobre ela.
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por john » Sáb Fev 19, 2011 23:00
por john » Sáb Fev 19, 2011 23:00
Estou tentando esta:
Provar que
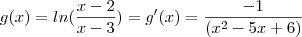
Eu fiz:

=
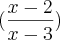
'
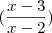
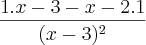
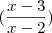
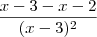
Depois simplifiquei. Cortei

com
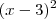
Fiquei com:
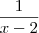
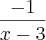
Multipliquei e fiquei com:
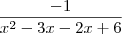
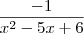
Está correcto? Fiz bem as regras?
Obrigado.
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Sáb Fev 19, 2011 23:23
por LuizAquino » Sáb Fev 19, 2011 23:23
john escreveu:Provar que se
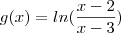
, então
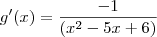
john escreveu:Está correcto? Fiz bem as regras?
Correto está, mas você deve tomar cuidado com a escrita, isto é, com a notação usada. Veja como seria a notação correta:
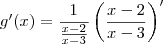
![g^\prime (x) = \frac{x-3}{x-2} \left[\frac{1\cdot(x-3)-(x-2)\cdot 1}{(x-3)^2}\right] g^\prime (x) = \frac{x-3}{x-2} \left[\frac{1\cdot(x-3)-(x-2)\cdot 1}{(x-3)^2}\right]](/latexrender/pictures/c7ea80086040152d739754365d444de5.png)
![g^\prime (x) = \frac{x-3}{x-2} \left[\frac{-1}{(x-3)^2}\right] g^\prime (x) = \frac{x-3}{x-2} \left[\frac{-1}{(x-3)^2}\right]](/latexrender/pictures/04e87793daaf171764631366016612a2.png)
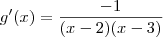
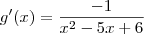
Uma escrita errada gera um resultado diferente do esperado. Por exemplo, você escreveu:
john escreveu: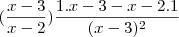
Do jeito que isso está escrito nós temos
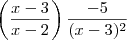
e não
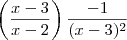
como era esperado.
Note que o uso dos parênteses faz toda a diferença na expressão
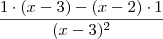
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por john » Dom Fev 20, 2011 00:01
por john » Dom Fev 20, 2011 00:01
Pois, tem toda a razão. Já num outro dia troquei valores por não colocar parênteses.
Agora tentando outro não consegui.
Provar que g''(x) da mesma função anterior é igual a
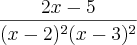
Eu estive fazendo e fiz isto:
g'(x)= ((-1)'.(x^2-5x+6))-((-1)(x^2-5x+6))/((x^2-5x+6)^2)
g'(x)= 0 - ((-1)*2x-5)/((x^2-5x+6)^2)
g'(x)= (2x-5)/((x^2-5x+6)^2)
Não consigo progredir mais. Pode-me ajudar?
Obrigado!
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Dom Fev 20, 2011 00:10
por LuizAquino » Dom Fev 20, 2011 00:10
john escreveu:g'(x)= (2x-5)/((x^2-5x+6)^2)
Não consigo progredir mais. Pode-me ajudar?
A questão está praticamente pronta! Lembra-se que
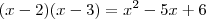
? Basta lembrar disso e você termina a questão.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por john » Dom Fev 20, 2011 00:13
por john » Dom Fev 20, 2011 00:13
LuizAquino escreveu:john escreveu:g'(x)= (2x-5)/((x^2-5x+6)^2)
Não consigo progredir mais. Pode-me ajudar?
A questão está praticamente pronta! Lembra-se que
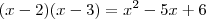
? Basta lembrar disso e você termina a questão.
Verdade. Obrigado.
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10896 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13200 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14806 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5116 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



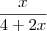 = f'(x)=
= f'(x)=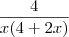
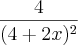
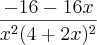
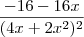
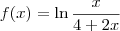 , calcule f'.
, calcule f'.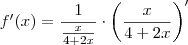
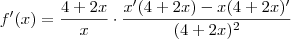
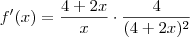
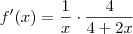
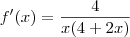
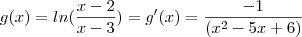
 =
=  '
'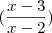
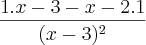
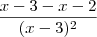
 com
com 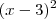
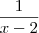
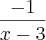
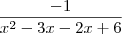
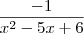
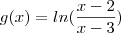 , então
, então 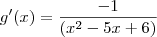
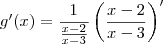
![g^\prime (x) = \frac{x-3}{x-2} \left[\frac{1\cdot(x-3)-(x-2)\cdot 1}{(x-3)^2}\right] g^\prime (x) = \frac{x-3}{x-2} \left[\frac{1\cdot(x-3)-(x-2)\cdot 1}{(x-3)^2}\right]](/latexrender/pictures/c7ea80086040152d739754365d444de5.png)
![g^\prime (x) = \frac{x-3}{x-2} \left[\frac{-1}{(x-3)^2}\right] g^\prime (x) = \frac{x-3}{x-2} \left[\frac{-1}{(x-3)^2}\right]](/latexrender/pictures/04e87793daaf171764631366016612a2.png)
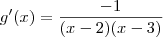
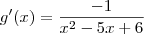
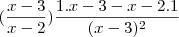
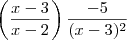 e não
e não 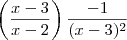 como era esperado.
como era esperado.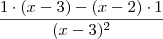 .
.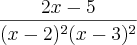
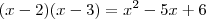 ? Basta lembrar disso e você termina a questão.
? Basta lembrar disso e você termina a questão. } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: