1. Uma pirâmide hexagonal regular tem aresta da base medindo 6cm. Se sua altura é de
10cm, qual será o comprimento de cada aresta lateral? Desenhe uma planificação para ela. (Você
pode usar o programa computacional Geogebra ou o Cabri Géomètre)
2. Um octaedro regular é seccionado na terça parte de suas arestas que concorrem em um
mesmo vértice e retiradas as pirâmides de base quadrada, resulta um poliedro arquimediano
composto por faces hexagonais regulares e faces quadradas chamado Octaedro truncado.
Dica: Procure descobrir se é possível usar a relação de Euler para achar o número de
vértices. Para o cálculo do número de diagonais, deduza uma expressão geral, partindo do
seguinte raciocínio: Considerando todos os vértices existentes no polígono, quantos
segmentos de retas podemos formar, sabendo que cada um destes segmentos é formado
por dois vértices? Deste número obtido, o que eu preciso retirar, para sobrar apenas as
diagonais do polígono?
a) Determine o número de vértices desse novo poliedro;
b) O número de diagonais desse novo poliedro;
c) determine a distância entre duas de suas faces quadradas opostas (paralelas). Para isto,
considere que, originalmente, cada aresta do octaedro regular media a cm.
.
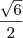, então teremos: 
cm de distância entre as faces hexagonais passando pelo centro... A primeira fórmula é encontrada nos livros e até mesmo no site do Wolfram.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)