Olá
ronaldy, boas-vindas!
Primeiro, revise como obter a área de um polígono regular de
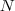
lados (
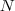
em letra maiúscula para não confundir com o

do enunciado, pois
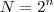
).
Você verá que será necessário considerar o apótema que é a distância perpendicular de um dos lados do polígono até o seu centro.
Para visualizar, divida alguns polígonos regulares em triângulos isósceles e, por Pitágoras, escreva a medida do lado em função do apótema.
Depois, na expressão da área (que deverá estar em função do apótema e do número de lados
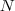
), reescreva o apótema somente em função de
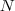
(já que a circunferência possui raio unitário).
Assim, com a expressão da área para os polígonoes regulares, somente em função de
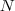
, você poderá representar alguns elementos da seqüência e prosseguir com sua análise.
Por favor, colabore com as regras para participação no fórum.
Bons estudos!


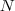 lados (
lados ( do enunciado, pois
do enunciado, pois 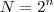 ).
).

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.