Eu resolvi o seguinte sistema de equações lineares:
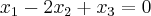

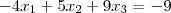
O sistema tem uma solução, que é (29, 16, 3).
Então eu pensei nessa solução como um ponto em R³, e em cada equação como uma reta em R³, que se encontram no ponto (29, 16, 3).
Daí o que eu fiz foi determinar um ponto qualquer para cada uma das equações, e obtive (2,1,0), (0,8,1) e (2,-2,1). Acredito que esteja na ordem da primeira à terceira equação.
Em seguida fiz a equação paramétrica de cada reta, obtendo primeiro o vetor (diminuindo o ponto qualquer de cada reta da solução do sistema) e em seguida montando cada equação:
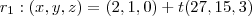
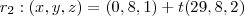

E por último joguei tudo no Winplot que fez o seguinte gráfico (clique na imagem para ampliar):

Eu girei e aproximei esse gráfico em todos os sentidos, e pelo gráfico eu fico seguro em afirmar que sim, as três retas se cruzam.
Agora, o que eu quero confirmar é se o procedimento e o raciocínio fazem sentido. Eu cheguei ao objetivo final que eu queria, que era ver as três retas se cruzando, mas em poucas palavras, equações lineares podem ser transformadas em equações paramétricas dessa forma? E o ponto onde elas se cruzam é realmente a solução do sistema


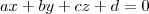 representa um plano no
representa um plano no 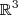 , e não uma reta.
, e não uma reta.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)