Integral

por **shark4ever** » Dom Jan 30, 2011 13:59

Saudações a todos,
Tenho desde ja uma duvida a qual agradeço desde ja a vossa ajuda.
Tenho a seguinte função
$f(x)=\int_{-2}^0 \frac{x+2}{4}dx + \int_{0}^{2} \frac{k-x}{4}dx$

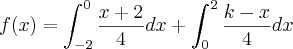
e pretendia obter o valor de K, nao sei se me estou a fazer entender.

cumpr

por **Molina** » Dom Jan 30, 2011 20:15

Boa noite, amigo.

Não ficou muito claro a exibição da integral.

Em cima uma aparece embaixo da outra.

Já na de baixo você as colocou como numa soma.

Tem como deixar mais claro como ela estão?

Abraços!

por **shark4ever** » Dom Jan 30, 2011 21:15

Não sei se agora ja esta mais claro.

Nao se sei o passo seguinte sera assim:

$=\int_{-2}^0 {\frac{1}{4}*(x+2)}dx + \int_{0}^2 {\frac{1}{4}*(k-x)}dx$

por **Elcioschin** » Seg Jan 31, 2011 10:12

Ainda não ficou claro

Tem-se uma função f(x) e quer-se descobrir o valor de K

Para isto deve ser dito qual é o valor de f(x), senão o problema é impossível

por **shark4ever** » Seg Jan 31, 2011 13:35

http://img832.imageshack.us/i/estatistica0000.png/

esta ai o exercicio

por **LuizAquino** » Qui Fev 03, 2011 08:48

O enunciado do exercício diz o seguinte:

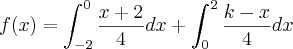
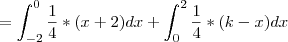
Considere a variável aleatória X com a seguinte função de probabilidade:
$f(x) = \left\{\begin{array}{ll} \frac{x+2}{4} &, -2\leq x < 0 \\ \frac{k-x}{4} &, 0\leq x \leq 2 \\ 0 &, \textrm{caso contr\'ario}\end{array}\right.$

a) Determine, justificando detalhadamente, o valor da constante k.

Para que uma função seja uma função de probabilidade ela deve ser sempre positiva e a integral em todo os seu domínio deve ser igual a 1.

O domínio dessa função é todo o conjunto dos números reais, então devemos ter:
$\int_{-\infty}^{+\infty} f(x)\,dx = 1$

Note que essa função está definida em intervalos, de modo que fora do intervalo [-2, 2] ela é zero. Portanto, podemos simplificar essa integral para:
$\int_{-2}^{2} f(x)\,dx = 1$

Por fim, a função tem uma expressão diferente para os intervalos [-2, 0) e [0, 2]. Portanto, temos que:
$\lim_{b\to 0^-}\int_{-2}^{b} \frac{x+2}{4}\,dx + \int_{0}^{2} \frac{k-x}{4}\,dx= 1$

Note que esse limite que apareceu na primeira integral é só para dar conta do fato que em x=0 a função está definida como (k-x)/4 e não como (x+2)/4.

Resolvendo as integrais, obtemos:
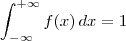
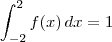
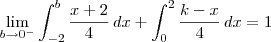
$\lim_{b\to 0^-} \frac{1}{4}\left[\frac{x^2}{2} +2x\right]_{-2}^b + \frac{1}{4}\left[kx - \frac{x^2}{2}\right]_0^2 = 1$

$\lim_{b\to 0^-} \frac{1}{4}\left[\frac{b^2}{2} +2b - \left(\frac{(-2)^2}{2} +2(-2)\right)\right] + \frac{1}{4}\left[2k - \frac{2^2}{2} - \left(0\cdot k - \frac{0^2}{2}\right) \right] = 1$

$\lim_{b\to 0^-} \frac{1}{4}\left[\frac{b^2}{2} + 2b + 2\right] + \frac{1}{4}(2k - 2) = 1$

$\frac{1}{2} + \frac{1}{4}(2k - 2) = 1$

k=2