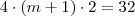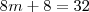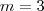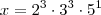heroncius escreveu:o número natural "X" decomposto em fatores primos se escreve na forma 2^3 x 3^m x 5. sabendo q "X" tem 32 divisores naturais, podemos afirmar q o n° de algarismos de sua represntação decimal é: a)3 b)5 c)7 d)4 e)6
com base nestas informações cheguei ao vlr de m=3, lgo o valor de x=1080...daí morri na praia.
Olá
heroncius!
Você concluiu que
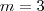
e
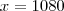
, o que praticamente já resolveu o problema, porque a representação decimal de 1080 possui 4 algarismos
(alternativa d).
Mas, de qualquer forma, acho importante comentar sobre
divisores naturais, assim como o percurso da conclusão.
De uma forma geral, se

é um número natural, decomposto em fatores primos, ele poderá ser escrito assim:
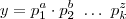
, onde

são números primos.
Um
divisor natural de

será, necessariamente, da forma:
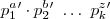
Sendo:
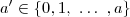
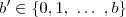

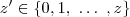
A conclusão é que temos

formas de escolher

,

formas de escolher
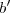
e

formas de escolher
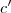
.
E por combinatória, o número de divisores naturais será:

Considerando o caso particular do exercício, temos que:
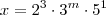
Ou seja, qualquer divisor natural de

será da forma:
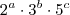
Onde,
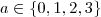
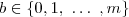
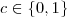
Donde podemos afirmar que temos 4 modos de escolher
a,

modos de escolher

e 2 modos de escolher

.
Por combinatória, podemos fazer a conta (lembrando que há 32 divisores naturais):
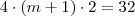
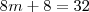

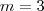
(apenas para detalhar de onde obtemos
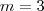
)
Como:
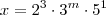
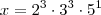
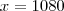
, de fato.
Com representação decimal de 4 algarismos.


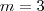 e
e 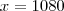 , o que praticamente já resolveu o problema, porque a representação decimal de 1080 possui 4 algarismos
, o que praticamente já resolveu o problema, porque a representação decimal de 1080 possui 4 algarismos  é um número natural, decomposto em fatores primos, ele poderá ser escrito assim:
é um número natural, decomposto em fatores primos, ele poderá ser escrito assim: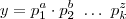 , onde
, onde  são números primos.
são números primos.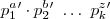
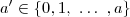
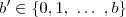

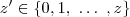
 formas de escolher
formas de escolher  ,
, formas de escolher
formas de escolher 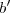
 formas de escolher
formas de escolher 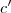 .
.
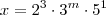
 será da forma:
será da forma: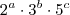
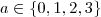
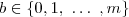
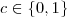
 modos de escolher
modos de escolher  e 2 modos de escolher
e 2 modos de escolher  .
.