Olá Baianinha,
Vejamos um exemplo. Vamos considerar a transformação linear
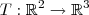
definida por
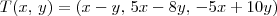
.
O núcleo (ou kernel) dessa transformação linear é definido como:
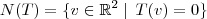
Portanto, precisamos resolver a equação:
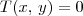
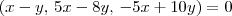
De onde obtemos o sistema:
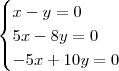
A única solução desse sistema é x=0 e y=0. Portanto o núcleo dessa transformação tem apenas um elemento, que é o (0, 0). Ou seja, diremos que:
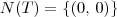
A imagem dessa transformação linear é definido como:
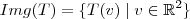
Para determinar a imagem podemos determinar uma base para a mesma.
Nesse exemplo, todos os elementos da imagem tem o formato (x-y, 5x-8y, -5x +10y). Note que qualquer elemento dessa imagem pode ser escrito como combinação linear dos vetores (1, 5, -5) e (-1, -8, 10):
(x-y, 5x-8y, -5x +10y) = x(1, 5, -5) + y(-1, -8, 10).
Portanto, o conjunto {(1, 5, -5), (-1, -8, 10)} gera a imagem. Se esse conjunto for L.I., então ele formará uma base para a imagem.
De fato, ele é L.I., pois a equação
k(1, 5, -5) + m(-1, -8, 10) = 0,
só possui uma única solução que é k=m=0.
Sendo assim, temos que:
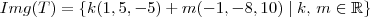


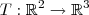 definida por
definida por 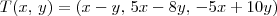 .
.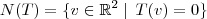
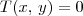
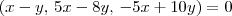
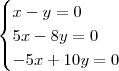
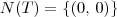
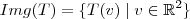
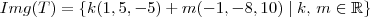



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.